0. 復習

ノイズキャンセリングイヤホン

　ノイズキャンセリングイヤホンは、様々な環境の中でもその音をキャンセルしなければならない（＝ 適応信号処理）。

その中身は適応信号処理で書かれている。（この動画シリーズはいろいろ解説しているので、興味があれば見てください）

最急降下法 (勾配法の一つ)

　ある関数について、その値を最小化（あるいは最大化）するようにパラメータを反復的に更新する数値計算法。最小化する関数を $f(x_1, x_2, \ldots, x_N)$、更新するパラメータを $\bm{x} = [x_1, x_2, \ldots, x_N]^\top$ とすると、最急降下法のアルゴリズムは以下で記述される。

1. 反復回数 $k$ を 0 に初期化。パラメータを $\bm{x}^{(k=0)} = [x_1^{(0)}, x_2^{(0)}, \ldots, x_N^{(0)}]^\top$ に初期化。

2. 勾配 $\bm{g} = \left[ \left. \frac{\partial f}{\partial x_1}\right|_{\bm{x}=\bm{x}^{(k)}}, \left. \frac{\partial f}{\partial x_2}\right|_{\bm{x}=\bm{x}^{(k)}}, \ldots, \left. \frac{\partial f}{\partial x_N}\right|_{\bm{x}=\bm{x}^{(k)}}\right]^\top$を求める。

3. パラメータを$\bm{x}^{(k+1)} = \bm{x}^{(k)} - \alpha \bm{g}$ で更新する（$\alpha$ はハイパーパラメータ）。$k$ を 1つ増やす。

4. 3. の更新量が大きければ 2. に戻る。

5. $\bm{x}^{(k)}$ を最終的なパラメータとする。

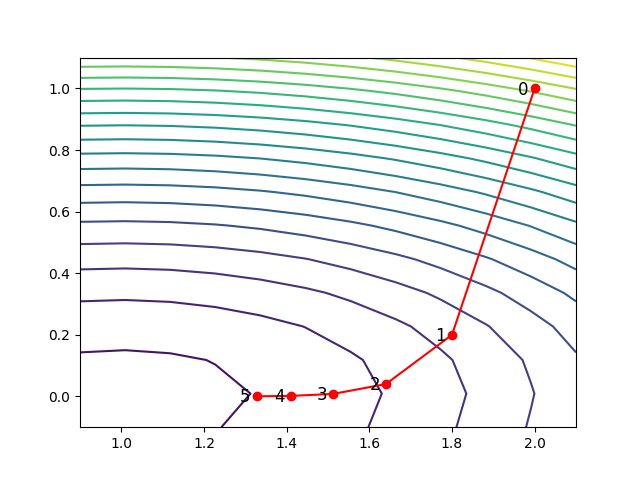
例題：$f(x) = x^2 - 2x + 4y^2$ を最小化するパラメータ $x, y$ を求めよ。

1. $k = 0$ に初期化、$x^{(0)} = 1, y^{(0)} = 0$ に初期化

2. 勾配を求める
   1. $\frac{\partial f}{\partial x}=2x-2, \frac{\partial f}{\partial y}=8y$

3. パラメータを更新する。
   1. $x^{(k+1)} = x^{(k)} - \alpha(2x^{(k)}-2),\;\; y^{(k+1)} = y^{(k)} - \alpha(8y^{(k)})$

4. (以下省略)

   

# 参考：上図のプロットに使ったコード
import numpy as np
import matplotlib.pyplot as plt

def f(x, y): # function
    return x**2 - 2*x + 4*y**2

def g(x, y): # gradient
    return 2*x - 2, 8*y

# for draw
X, Y = np.meshgrid(np.linspace(0.9, 2.1, 12), np.linspace(-0.1, 1.1, 12))
cont = plt.contour(X, Y, f(X, Y), 20) 

# gradient descent
k = 0
x, y = 2, 1
alpha = 0.1
x_hist, y_hist = [x], [y]

for i in range(5):
    # gradients
    dx, dy = g(x, y)
    
    # update
    x -= alpha * dx
    y -= alpha * dy
    k += 1

    # for draw
    x_hist.append(x)
    y_hist.append(y)

# draw
plt.plot(x_hist, y_hist, 'ro-')
for k, (x, y) in enumerate(zip(x_hist, y_hist)):
    plt.text(x - 0.04, y - 0.02, f'{k}', fontsize=12)
plt.savefig('plot.png')

　この図から

• 適切な $\alpha$ を設定できる

• 良い初期値からスタートできる

ならば良い解にたどり着けることがわかる。これは、関数が合成関数であろうと同様に実行可能である（＝ニューラルネットワークの学習）。

1. 適応信号処理　

“適応”する信号処理

　下図のようなノイズキャンセリングヘッドホンを考えよう。

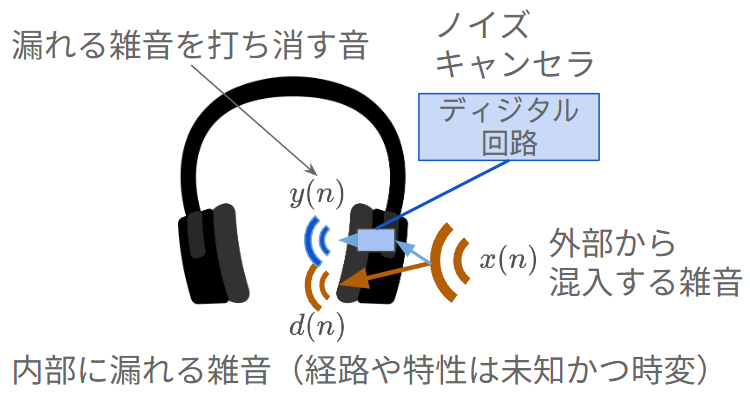
ヘッドホンの外で雑音（例えば、人混み、電車）$x(n)$ がなっている。この雑音の一部はヘッドホン内部に漏れ、$d(n)$ として鼓膜に伝わる。このとき、$x(n)$ と $d(n)$ の間の伝達特性は未知かつ時変とする（例えば、人の頭の形によってヘッドホンの装着具合は異なるし、その装着具合も時々刻々と変化する）。

　この漏れ聞こえる雑音を除去したい（＝ノイズキャンセリング）。このためにヘッドホン内部にディジタル回路を用意する。このディジタル回路のパラメータ（フィルタ係数）は制御可能とし、$x(n)$ の入力に対し何らかの出力 $y(n)$ を出力する。この出力 $y(n)$ はスピーカを通じてヘッドホン内部に再生される。このとき、 $d(n)$ と $y(n)$ が逆相、すなわち $y(n)=-d(n)$ となれば漏れ聞こえる雑音は 0 となる。

　これを実現するフィルタとして FIR フィルタを考える。

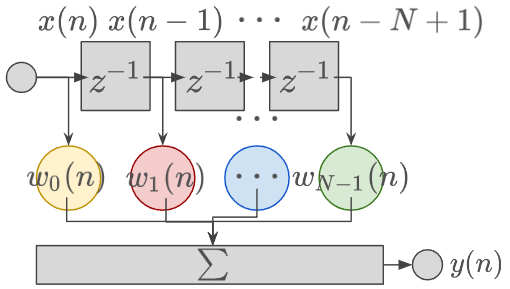
過去の $N$ サンプルを用いて $y(n)$ を出力する。フィルタ係数は、$w_0(n), w_1(n), \ldots, w_{N-1}(n)$ の $N$ 個である。ここで、$d(n)$ の特性は時変であるため、その効果を打ち消すフィルタも時変であるべきである。そのため、フィルタ係数に $"(n)"$ をつけて係数が時変であることを表す。式で表すと、

である（総和範囲が教科書と 1 ずれていることに注意する）。このとき、打ち消したい信号との差の二乗、すなわち、

を最小化するようにフィルタ係数を決定すればよい。

　フィルタ係数を決定するうえで、満たしたほうが良い条件がいくつかある。

1. 雑音を高精度に除去できること

2. フィルタ係数の計算量が小さいこと
   1. フィルタ係数を時々刻々と決定するため、定められた更新タイミング内で終了する計算量でなければならない。例えば 0.1 秒ごとにフィルタ係数を更新したいのに、その計算に 1 秒かかっては使い物にならない。

3. (本講義では触れないが) 被対象音の混入に対して頑健であること

線形予測は使えないのか？

　前回の講義で線形予測 (linear prediction) を習った。この方法でフィルタ係数を求めればよいのではないだろうか？

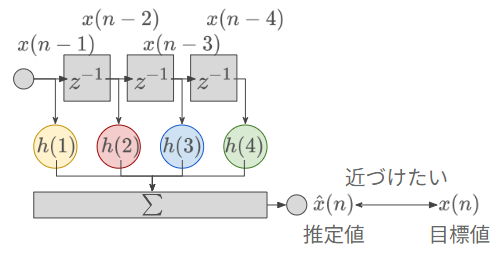
　確かにこの方法を使えば、フィルタ係数を解析的に求められる。しかしながら、この方法は計算業が大きい。このフィルタ係数 $h$ は以下の行列の式を解くと求められる。$\phi_{xx}$ は自己相関関数である。

この計算は、

• 自己相関関数の計算： 長さ $N$ の信号に対して $N^2$ の計算量

• 逆行列の計算：長さ $N$ の信号に対して $N^3$ の計算量

を要請される。そのため、計算量を抑えたい目的にそぐわない。

(余談) 上記の計算量はあくまでナイーブに計算したときの計算量である。例えば、

• 高速フーリエ変換（FFT）を持ちいた自己相関関数の計算 → $N\log N$ の計算量

• Levinson-Durbinアルゴリズムを用いた逆行列の計算 → $N^2$ の計算量

のように計算量を抑えられる。興味のある方は調べてほしい。

勾配法（最急降下法）を用いて更新しよう

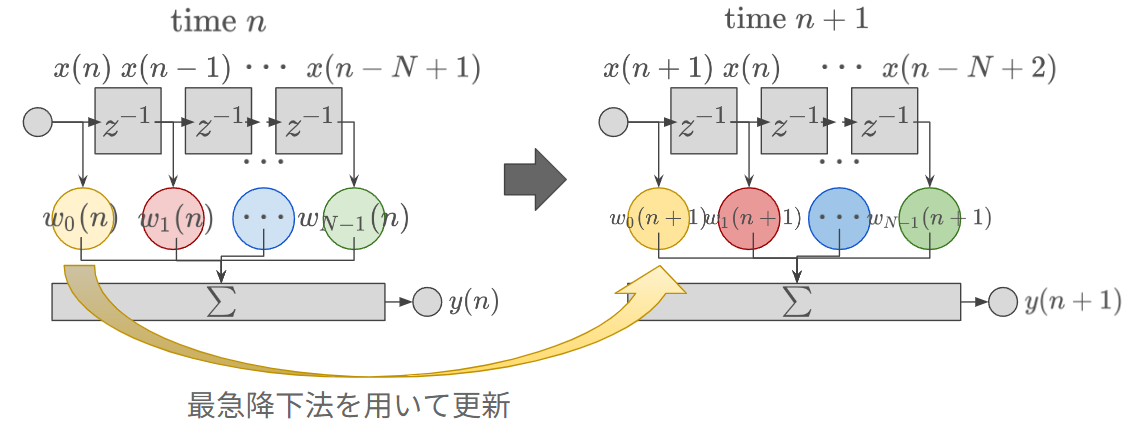
　前述したように、勾配法なら計算量が少なくて済む。具体的には、

• 最小化される関数は目標値と予測値の誤差関数の2乗

• 更新されるパラメータは、適応信号処理におけるフィルタ係数

• 初期パラメータは、前時刻のパラメータ

である。これを踏まえてフィルタ係数の勾配を求めてみる。誤差関数の2乗は、

　であり、この微分は、

となる。すなわち更新式は、

となる。$\alpha$ を適切に設定できれば、この式によって更新が可能（同じ時刻でこの反復を繰り返すことも可能）。この式は、

• $k$ 番目のフィルタ係数の勾配は、以下の2つがわかればよい。
  • $k$ 遅れの入力 $x(n-k)$
  • 誤差 $d(n) - \sum\limits_{k=0}^{N-1}w_{k}(n)x(n-k)$ （過去の入力とフィルタ係数の積和）

• すなわち、非常に簡単にフィルタ係数を更新できる

2. まとめ

• 適応信号処理では、フィルタ係数を勾配法で更新する

• 目的関数を誤差の2乗としたとき、勾配法に用いる勾配は誤差と入力信号の積となる。

3. 次回(演習)・次々回(期末試験)について

• 次回
  • 演習。いつも通り教室に集まってください。
  • 期末試験に向けてその内容をしっかり理解すること。
  • 周りと話し合いながら演習を進めてください。質問はいつでも受け付けています。
  • 回答は授業開始後 60 分後くらいに公開します。
  • 授業後課題はありません

• 次々回
  • 筆記試験です。演習の内容を理解しておいてください。