ディジタル信号処理第11回-2 線形予測

💡

過去の信号の情報から次の時刻の信号を予測しよう。

0. イントロダクション

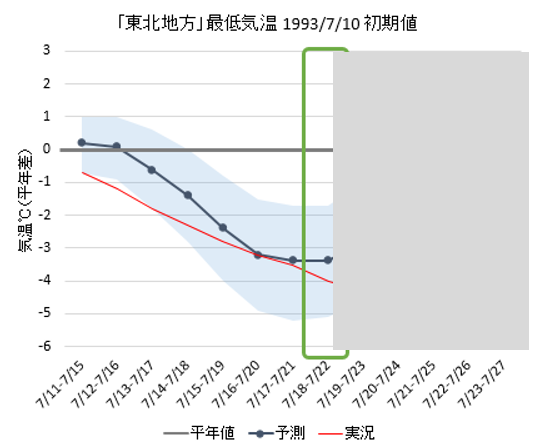
この図は、1993年における最低気温の推移である（https://www.data.jma.go.jp/risk/probability/info/kakodata_kensho.html の画像を一部改変）。これまでに分かっている7/22までの推移を踏まえると、7/23の最低気温は 7/22 の最低気温より上がるだろうか？下がるだろうか？

💡

気温は上がる？下がる？ slido 上で回答。

　おそらく多くの意見が一致したはずだ。なぜわかるのだろうか？それは我々人間がこれまでの経験（＝データ）から学習しているからだ。では、我々と同じように「データから学習して次を予測する信号処理」を作ってみよう。

💡

皆が別講義で習ったように、データから学習することは機械学習の技術であるように見える。確かにそのとおりで、この学習は機械学習でもあり信号処理でもある。信号処理と機械学習は排他的なものではない。

1. 最小二乗誤差に基づく線形予測

定義

　推定したい現在の値が、過去の値から線形に予測できると仮定する。すなわち、過去の値 $x(n-1), x(n-2), \ldots, x(n-N)$ を用いて現在の予測値 $\hat x(n)$ を予測する次式

\begin{align} \hat x(n) &= - h(1)x(n-1) - h(2)x(n-2) - \ldots - h(N)x(n-N) \\ &= \sum\limits_{n=1}^{N}h(k)x(n-k) \end{align}

を用いる。このような式で予測すること方法を線形予測 (linear prediction) と呼ぶ。

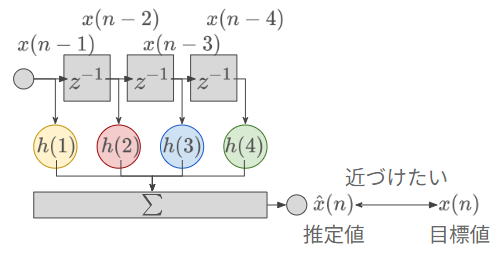
　この式は FIR フィルタの式に似ているが、取り組む問題は異なる。これまでの講義の FIR フィルタでは「入力 $x(n)$ とフィルタ係数 $h(x)$ が既知のもとで、出力 $y(n)$ を求めなさい」という順問題を扱ってきた。一方でこの線形予測では、「入力 $x(n-1), x(n-2), ...$ と目標の出力 $x(n)$ が既知のもとで、フィルタ係数（＝パラメータ） $h(x)$ を求めなさい」という逆問題を解くことになる。

　（余談）

順問題：入力、関数が既知 → 出力を求める問題

逆問題：入力、出力が既知 → 関数を求める問題

(図は https://www.nda.ac.jp/cc/users/iwase/OLD/EDU/JUGYO/2000/TOMO/tomo/node4.html から引用)

パラメータ（＝フィルタ係数）を求める

目的関数を設定

　パラメータは、何らかの評価関数の値を最小化（あるいは最大化）するように決定されるのが一般的である。線形予測における評価関数とは、目標値と推定値の近さに関する関数であり、近づくほどのその値が小さくなる。

　ここでは評価関数として、時刻 $1, 2, \ldots, N$ における目標値と推定値の二乗誤差の和として次式を定める。

\begin{align} J &= \sum\limits_{i = 1}^{N} \left(x(i) - \hat x(i) \right)^2 \\ &= \sum\limits_{i = 1}^{N} \left(x(i) - \sum\limits_{k = 1}^{N}h(k)x(i-k) \right)^2 \end{align}

　この関数の値を最小化するように $h(1), h(2), \ldots, h(N)$ を求めよう。この式は $h(1), h(2), \ldots, h(N)$ のそれぞれについて2次式である。すなわち、この式を微分して 0 としたときの $h(1), h(2), \ldots, h(N)$ が解析的な答えとなる。

微分してパラメータを求める

式(3)を、 $j$ 番目のパラメータ $h(j)$ について微分して 0 とおくと、

\begin{align} \frac{\partial J}{\partial h(j)} &= 2\sum\limits_{i=1}^{N}\left\{ \left(x(i) - \sum\limits_{k = 1}^{N}h(k)x(i-k) \right)\cdot x(i-j)\right\} \\ &\propto \sum\limits_{i=1}^{N} x(i)x(i-j) - \sum\limits_{k=1}^{N}h(k)\sum\limits_{i = 1}^{N}x(i-k)x(i-j) \\ &= 0 \end{align}

となるここで自己相関関数の定義

\begin{align} \phi_{xx}(m) = \frac{1}{N}\sum\limits_{n = 0}^{N-1}x(n)x(n+m) \end{align}

を代入する。さらに自己相関関数が偶関数であることを利用する（x(n) が 0 始まりか 1 始まりかが混合しているが、全体を1シフトすれば等価なので無視してよい）と

\begin{align} \frac{1}{N}\phi_{xx}(j) - \frac{1}{N}\sum\limits_{k=1}^{N}h(k)\phi_{xx}(k-j) &= 0 \\ \sum\limits_{k=1}^{N}h(k)\phi_{xx}(k-j) &= \phi_{xx}(j) \end{align}

この式は、 $j$ 番目のパラメータ $h(j)$ について微分して 0 としたものであるため、同様に、すべてのパラメータについて求めると最終的に行列表現が得られる。

\left[\begin{array}{cccccccc}\phi_{xx}(0) & \phi_{xx}(1) & \phi_{xx}(2) & \phi_{xx}(3) & \phi_{xx}(4) & \phi_{xx}(5) & \phi_{xx}(6) & \phi_{xx}(7) \\\phi_{xx}(1) & \phi_{xx}(0) & \phi_{xx}(1) & \phi_{xx}(2) & \phi_{xx}(3) & \phi_{xx}(4) & \phi_{xx}(5) & \phi_{xx}(6) \\\phi_{xx}(2) & \phi_{xx}(1) & \phi_{xx}(0) & \phi_{xx}(1) & \phi_{xx}(2) & \phi_{xx}(3) & \phi_{xx}(4) & \phi_{xx}(5) \\\phi_{xx}(3) & \phi_{xx}(2) & \phi_{xx}(1) & \phi_{xx}(0) & \phi_{xx}(1) & \phi_{xx}(2) & \phi_{xx}(3) & \phi_{xx}(4) \\\phi_{xx}(4) & \phi_{xx}(3) & \phi_{xx}(2) & \phi_{xx}(1) & \phi_{xx}(0) & \phi_{xx}(1) & \phi_{xx}(2) & \phi_{xx}(3) \\\phi_{xx}(5) & \phi_{xx}(4) & \phi_{xx}(3) & \phi_{xx}(2) & \phi_{xx}(1) & \phi_{xx}(0) & \phi_{xx}(1) & \phi_{xx}(2) \\\phi_{xx}(6) & \phi_{xx}(5) & \phi_{xx}(4) & \phi_{xx}(3) & \phi_{xx}(2) & \phi_{xx}(1) & \phi_{xx}(0) & \phi_{xx}(1) \\\phi_{xx}(7) & \phi_{xx}(6) & \phi_{xx}(5) & \phi_{xx}(4) & \phi_{xx}(3) & \phi_{xx}(2) & \phi_{xx}(1) & \phi_{xx}(0) \\\end{array}\right] \left[\begin{array}{cccccccc} h(1) \\ h(2) \\ h(3) \\ h(4) \\ h(5) \\ h(6) \\ h(7) \\ h(8) \\\end{array}\right] = \left[\begin{array}{cccccccc} \phi_{xx}(1) \\ \phi_{xx}(2) \\ \phi_{xx}(3) \\ \phi_{xx}(4) \\ \phi_{xx}(5) \\ \phi_{xx}(6) \\ \phi_{xx}(7) \\ \phi_{xx}(8) \\\end{array}\right]

（萩原先生の教科書では右辺に負記号がついている。上記の式展開で $h(n) \leftarrow - h(n)$ とすれば教科書に従った表記になる。）

　この式は Yule −Walker 方程式と呼ばれる。パラメータを求めるために逆行列を素直に求めてもよいが、Levinsonアルゴリズムな高速な解法も存在する。

2. まとめ

線形予測とは、過去の時刻の信号から現在の信号を線形の式で求める方法である。

線形予測係数は、行列を用いて求められる。