0. 2つの信号の「似ている度」をどう定量化する？

上記動画の1:08頃から始まるバスドラムの音を考えてみよう．

ケース1：異なる2つの信号

この 2 つの信号の「似ている度」をどうやって計算したら良いだろうか？

(音引用元： https://maou.audio/se_inst_drum1_kick/)

　直感的に良さそうなのは，各時刻について信号を掛けて，それを総和する方法．信号をそれぞれ $x(n), y(n)$ とすると，

例えば，

• 2 つの信号が同時に大きくなれば，似ている度も上がりそう

• 2 つの信号の符号が {正, 正} だったり {正, 負} だったりすると，似ている度は下がりそう

ケース2：時刻のズレた信号同士

　波形の形は似ている．ただ，波形の現れるタイミングが違うから式(1)でやっても測れなさそう．言い換えると，下の波形を左側にいい感じにシフトしてあげれば，ケース1と同じようになって式(1)で測れそう．

ケース3：自分自身

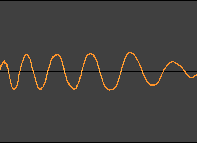
　自分自身と式(1) を計算すると，

のように 2乗和（＝パワー）になる．また，時間をずらした自分自身を計算すると，上図で信号の山谷のタイミングが揃う程度にずらしたときに，似ている度が大きくなりそう．

ケース1〜3を通して言えそうなこと

• 信号同士を掛けて足すと，似ている信号同士の「似ている度」が大きくなりそう

• 片方の信号をずらすと「似ている度」が変わるケースがある（＝「似ている度」はずらした数に依存した関数になりそう）

• 自分自身との「似ている度」を図っても，何かが得られそう

1. 自己相関関数・相互相関関数

定義

　相関関数とは、2つの信号（あるいは系列）の一致度を測る関数である。この関数は、片方の信号に対してずらした時間を引数にして、その時の信号間の一致度を返す。2 つの異なる信号$x, y$間で測る相関関数を相互相関関数という。

　$m$ はずらした時間値である。この式は、信号 $y$ を時刻 $m$ だけずらした時の、信号同士を掛けて総和したもの（＝式(1)）である。イメージは以下のとおり。

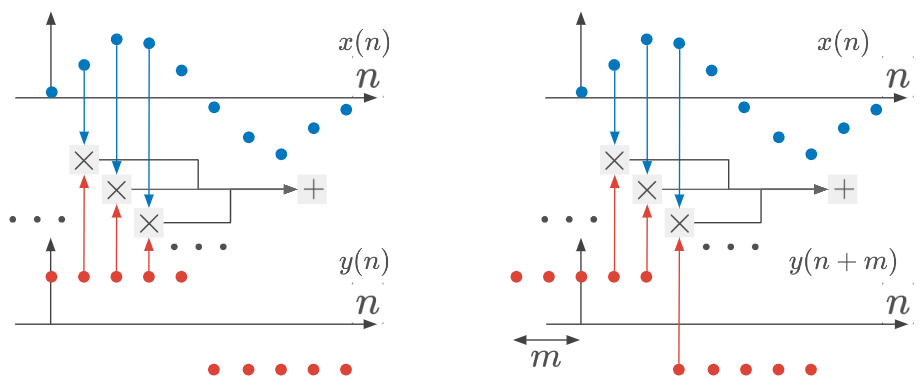
　一方で、1つの信号の中で計算される相関関数を自己相関関数という。

この式は、自分自身を時刻 $m$ だけずらした時の、自分同士を掛けて総和したもの（＝式(1)）。定常信号（平均や分散などの統計的性質が時間で変化しない信号）では偶関数になる（$\phi_{xx}(m) = \phi_{xx}(-m)$）。

手計算してみよう

2. まとめ

• 相関関数とは、片方の信号の時刻をずらしたときに、2つの信号の一致度を測る関数である。

• 関数の値は正規化されておらず、0 ~ 1 の値を超えることがある。一致するほど値が大きい。

• 周期的な信号の場合の自己相関関数は、周期に一致するときに大きくなる。