ディジタル信号処理09回 FIRフィルタ

💡
前回、IIR (無限インパルス応答) をやった。それと対をなすのが FIR フィルタである。その設計を学ぼう。

0. 復習

FIR フィルタと IIR フィルタ

伝達関数の形によってフィルタ（システム）は 2 種類に分類される。

Y(z)=H(z)X(z),    H(z)=Y(z)X(z)\begin{align} Y(z) = H(z) X(z),\;\; H(z) = \frac{Y(z)}{X(z)} \end{align}

となる。連続時間信号の場合はラプラス変換 (s変換) であり、上式の z が s になった式が導かれる。この H(z)H(z)  がシステムの伝達関数である。この伝達関数の式の形によって分類すると以下のようになる。

IIR (infinite impulse response) フィルタ

過去の時刻の出力が入力側に戻って、現在の時刻の出力を決める形

H(z)=b0+∑k=1Jbkz−k1+∑k=1Iakz−kH(z) = \frac{b_0 + \sum\limits_{k = 1}^{J}b_k z^{-k}}{1+\sum\limits_{k = 1}^{I}a_kz^{-k}}

FIR (finite impulse response) フィルタ

出力は入力側に戻らず、入力のみで現在の時刻の出力が決まる形

H(z)=b0+∑k=1Jbkz−kH(z) = b_0 + \sum\limits_{k = 1}^{J}b_k z^{-k}
https://www.youtube.com/shorts/1z-iolnj12U

残響（エコー）：壁に反射した音が再びマイクに収音される（＝出力された音が、時間遅れでもう一度出力される）

直線位相

　直線位相とは位相特性が直線であることである。フィルタが直線位相フィルタであるとき，フィルタリングによる波形の崩れは生じない。これを直感的に理解するために，周波数の異なる2つの正弦波を考える．

sin⁡(ω1t),sin⁡(ω2t)\sin\left( \omega_1 t \right), \sin\left( \omega_2 t \right)

この両方が時間 τ\tau だけ遅れるとする．すなわち，

sin⁡(ω1(t−τ))=sin⁡(ω1t−ω1τ)sin⁡(ω2(t−τ))=sin⁡(ω2t−ω2τ)\begin{align} \sin\left(\omega_1 (t - \tau) \right) &= \sin\left(\omega_1 t - \omega_1\tau \right) \\ \sin \left(\omega_2 (t - \tau) \right) &= \sin \left(\omega_2 t - \omega_2\tau \right) \end{align}

である．この時の位相特性はそれぞれ −ω1τ,−ω2τ-\omega_1\tau, -\omega_2\tau である．すなわち、位相特性が ω\omega に比例する（＝線形位相になる）。以上をまとめると、線形位相は、①位相特性が周波数に比例することであり、②時間遅れが周波数間で一定であることと等価であり、③(直感的に言えば) フィルタリングによる位相ずれを起こさないことである。また、①のとき群遅延（位相特性の周波数微分）は定数になるため、線形位相は④群遅延が定数になることでもある。

1. FIR フィルタの利点欠点、挙動

利点・欠点

利点

欠点

挙動

インパルスが入力された時のFIRフィルタの出力を考えよう．この出力はインパルス応答と一致する．

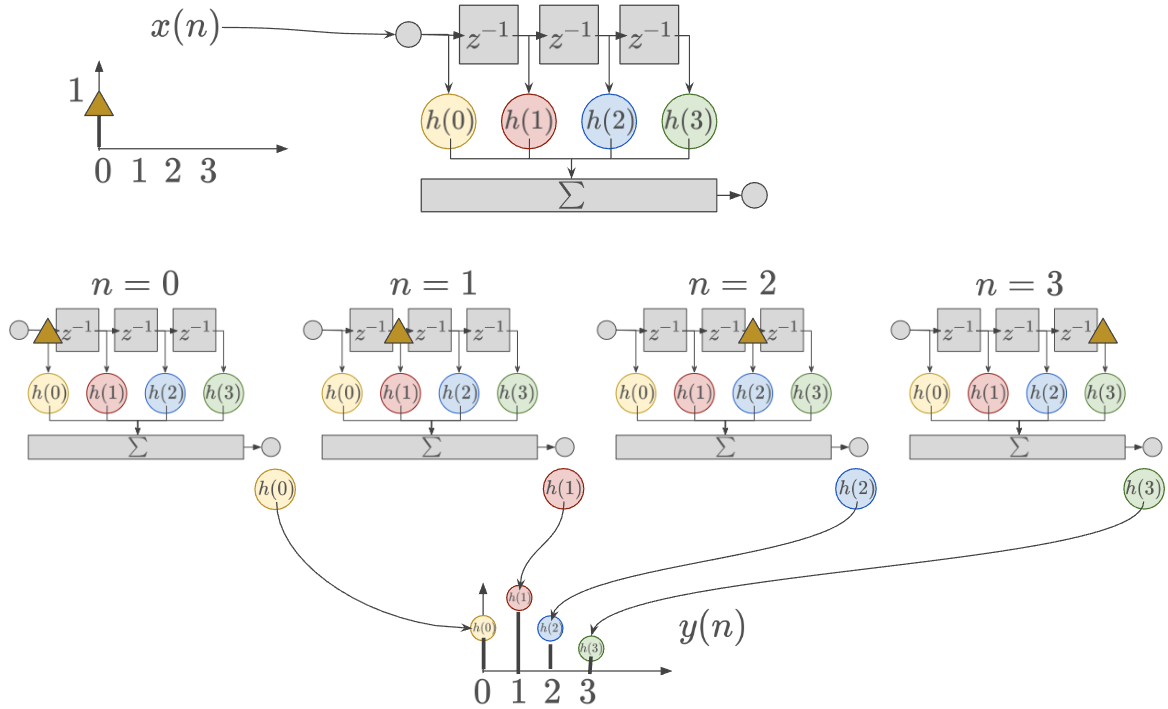
この図のとおり、フィルタの係数がわかれば、自動的にインパルス応答も計算できることになる。インパルスに限らず任意の入力に対しても同様に畳み込みで計算できる．

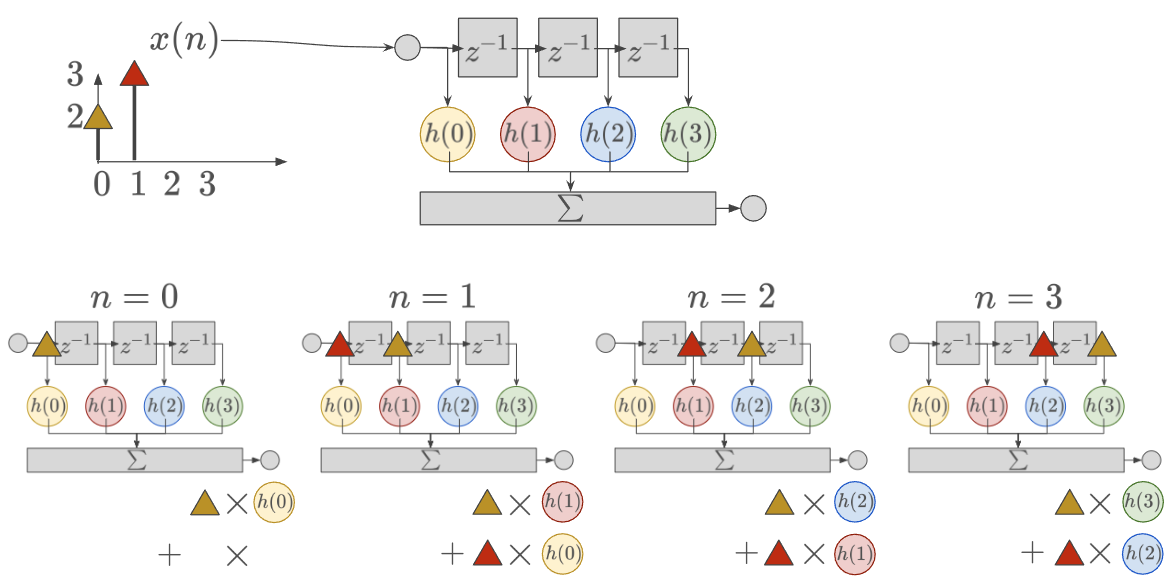
2. 直線位相を持つFIRフィルタとは

零位相フィルタ

　ここまで、フィルタは直線位相であることが望ましいことに触れた。では、直線位相であるフィルタとはどういうフィルタだろうか。

　これを考えるために、まずは零位相のフィルタ (zero-phase filter) を考える。すなわち、フィルタにおいて全ての波が時刻 0 に現れるフィルタ（すべての周波数の位相特性が 0 にフィルタ、すなわち、時刻遅れを生じさせないフィルタ）である。当然ながら、零位相フィルタは位相遅れがない（全周波数で0）ため直線位相フィルタである。

💡
位相特性が 0 のとき、インパルス応答は偶関数になることを示せ。ヒント：x(t)=∫−∞∞X(ω)ejωtdωx(t) = \int_{-\infty}^{\infty}X(\omega)e^{j\omega t} d\omega の式においてx(t)=x(−t)x(t)=x(-t) であることを示せばよい。（問題ではないが、この逆も実は成り立つ。すなわち、インパルス応答が偶関数なら位相特性は 0 である。）

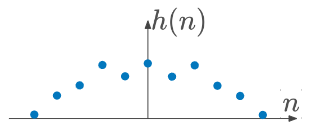
　補足：インパルス応答が偶関数であるということは、そのインパルス応答は cos のみで表現できる（sin成分の大きさは 0）ことを表す。補足すると、cos は偶関数であるため、その和で表現される関数もやはり偶関数である。
　話をもとに戻すと、零位相フィルタは時刻 0 を中心に偶対称（＝偶関数）である。

零位相フィルタから線形位相フィルタへ

　では、この零位相フィルタを 1 サンプルだけ動かすことを考える。全体が 1 サンプルだけずれるだけなので、このフィルタによる時刻遅れはすべての周波数で 1 サンプル分である。故に、このフィルタもやはり直線位相フィルタになる。

（補足）数式でもこれは説明できる。少しややこしいが離散時間ではなく連続時間で考える（離散時間で考えないのは、零位相フィルタの時間範囲と離散フーリエ変換の時間範囲が対応しないから）。インパルス応答h(t)h(t)と、それをτ\tauずらしたもの h(t−τ)h(t-\tau)を考える。これらのフーリエ変換を H(ω),H′(ω)H(\omega), H'(\omega) とすると、H′(ω)=H(ω)e−jωτH'(\omega)=H(\omega)e^{-j\omega\tau} の関係になる。これは、 h(t−τ)h(t-\tau) のフーリエ変換において、u=t−τu=t-\tau と変数変換すると導かれる。

　この議論は、全体を m サンプルずらした場合でも成り立つ。これらより、インパルス応答がその時刻中心から偶対称であれば、直線位相であることがわかる。

　ではこれを証明しよう。以下のようなインパルス応答（長さNN）を考える。このインパルス応答は中心で偶対称、すなわち h(n)=h(N−1−n)h(n) = h(N-1-n) である。ただし、NN は奇数とする。

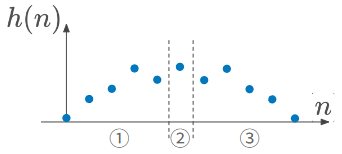
この z 変換は、

H(z)=∑n=0N−1h(n)z−n=∑n=0N−12−1h(n)z−n+h(N−12)z−N−12+∑N−12+1N−1h(n)z−n\begin{align} H(z) &= \sum\limits_{n=0}^{N-1}h(n)z^{-n} \\ &= \sum\limits_{n=0}^{\frac{N-1}{2}-1}h(n)z^{-n} + h\left(\frac{N-1}{2}\right)z^{-\frac{N-1}{2}} + \sum\limits_{\frac{N-1}{2}+1}^{N-1}h(n)z^{-n} \end{align}

ここで、右辺第1項, 2項, 3項をそれぞれ①②③とおく。③の総和範囲は、

N−12+1≤n≤N−1−N−12−1≥−n≥−(N−1)N−12−1≥N−1−n≥0\begin{align} \frac{N-1}{2}+1 \leq n \leq N -1 \\ -\frac{N-1}{2}-1 \geq -n \geq -(N -1) \\ \frac{N-1}{2}-1 \geq N-1-n \geq 0 \end{align}

と変形できるため、これを③に代入し、さらに偶関数の式を代入すると

③＝∑n=0N2−1h(N−1−n)z−(N−1−n)=∑n=0N2−1h(n)z−(N−1−n)\begin{align} ③&＝\sum\limits_{n=0}^{\frac{N}{2}-1}h(N-1-n)z^{-(N-1-n)} &= \sum\limits_{n=0}^{\frac{N}{2}-1}h(n)z^{-(N-1-n)} \end{align}

となる。ここで①③はそれぞれ、

①=∑n=0N−12−1h(n)z−n=z−N−12∑n=0N−12−1h(n)z−n+N−12③=∑n=0N2−1h(n)z−(N−1−n)=z−N−12∑n=0N2−1h(n)z−(−n+N−12)\begin{align} ① &= \sum\limits_{n=0}^{\frac{N-1}{2}-1}h(n)z^{-n} = z^{-\frac{N-1}{2}} \sum\limits_{n=0}^{\frac{N-1}{2}-1}h(n)z^{-n+\frac{N-1}{2}} \\ ③ &= \sum\limits_{n=0}^{\frac{N}{2}-1}h(n)z^{-(N-1-n)} = z^{-\frac{N-1}{2}} \sum\limits_{n=0}^{\frac{N}{2}-1}h(n)z^{-(-n+\frac{N-1}{2})} \end{align}

のように変形でき、①③のべき乗数が符号の異なる数になることがわかる。ここで①②③それぞれで z−N−12z^{-\frac{N-1}{2}} が出現したので、①②③をこの数でくくると

H(z)=z−N−12{∑n=0N−12−1h(n)z−n+N−12+h(N−12)+∑n=0N2−1h(n)z−(−n+N−12)}H(z)=z^{-\frac{N-1}{2}} \left\{ \sum\limits_{n=0}^{\frac{N-1}{2}-1}h(n)z^{-n+\frac{N-1}{2}} + h\left(\frac{N-1}{2} \right) + \sum\limits_{n=0}^{\frac{N}{2}-1}h(n)z^{-(-n+\frac{N-1}{2})} \right\}

ここから周波数特性を求めるために z=ejωTz = e^{j\omega T} を代入すると

H(ejωT)=e−jωN−12T{h(N−12)+∑n=0N−12−1h(n)[e−jω(n−N−12)T+ejω(n−N−12)T]}=e−jωN−12T{h(N−12)+2∑n=0N−12−1h(n)cos⁡(ω(n−N−12)T)}\begin{align} H(e^{j\omega T})&=e^{-j\omega\frac{N-1}{2}T} \left\{ h\left(\frac{N-1}{2} \right) + \sum\limits_{n=0}^{\frac{N-1}{2}-1}h(n)\left[e^{-j\omega(n-\frac{N-1}{2})T} + e^{j\omega(n-\frac{N-1}{2})T} \right] \right\} \\ &= e^{-j\omega\frac{N-1}{2}T} \left\{ h\left(\frac{N-1}{2} \right) + 2\sum\limits_{n=0}^{\frac{N-1}{2}-1}h(n)\cos\left(\omega(n-\frac{N-1}{2})T \right) \right\} \end{align}

故に、振幅特性・位相特性・群遅延は以下の通りとなる。

群遅延は遅延サンプル数に対応するため、このフィルタは、すべての周波数で (N−1)/2(N-1)/2サンプル遅延する直線位相フィルタである。

💡
N が偶数のときにも、インパルス応答が中心時刻から偶対称であれば、そのフィルタは直線位相フィルタであることを示せ。

3. まとめ