💡
IIRのアナログフィルタを設計できた。ディジタル計算機でこのフィルタを使いたいが、どうしたらいいだろうか? 2 つの方法を紹介する。
0. アナログフィルタ vs. ディジタルフィルタ
復習1:フィルタの種類
- 低域通過フィルタ (low pass filter, LPF):低い周波数を通過 (pass) させ,高い周波数を遮断 (cut) するフィルタ.高い周波数を遮断することを強調してハイカットフィルタとも言う
- 高域通過フィルタ (high pass filter, HPF):高い周波数を通過させ,低い周波数を遮断するフィルタ。低い周波数を遮断することを強調してローカットフィルタとも言う
- 帯域通過フィルタ (band pass filter, BPF):特定の中間帯域を通過させるフィルタ
- 帯域遮断フィルタ (band elimination filter, BEF):特定の中間帯域を遮断させるフィルタ
- 全域通過フィルタ (all pass filter, APF):全周波数帯域において同一ゲインで通貨させるフィルタ
アナログとディジタルの違い:フィルタにおいて
アナログフィルタ (動画では6秒あたりのペダル)。比較的安価な部品で作れ、連続信号のまま扱える(遅延が非常に小さく)。
ディジタルフィルタ。変更をかけやすい。数値誤差はのるが、設計の自由度が高いため誤差を小さくしやすい
💡
アナログフィルタで良いものができたとして、それと同じ効果を持つディジタルフィルタを作れないか?今回は IIR フィルタに限定して議論。
2つの方法を紹介。ざっくりいうと
- インパルス不変法:めちゃくちゃ簡単だけど使用に注意が必要
- 双一次変換:安全に使えるけどちょっと難しい
復習2:インパルス応答
あるシステムを考える。その特性はインパルス応答 (impulse response) で記述できる。インパルス応答とは、デルタ関数で記述されるインパルス信号に対して、そのシステムが出力する時間波形である。
デルタ関数を離散時間で表現すると
δ(n)={10n=0n=0 同様に連続時間で表すと
δ(t)={∞0t=0t=0,∫t=−∞∞δ(t)dt=1 である。ちなみに、上式の定義は厳密には不正確である。厳密な定義を知りたい方は「デルタ関数 超関数」などで調べるとよい。
💡
インパルス信号は、すべての周波数成分が 1 である(すなわち、全周波数の成分を同程度に持っている)信号である。
入力信号が与えられたときの出力信号は畳み込みで計算できる。離散時間の入力信号を x(n)、出力信号を y(n) とすると、その関係は
y(n)=h(n)∗x(n) で計算できる。x(n)=δ(n)、すなわちインパルス信号が入力されたとき、
y(n)=h(n)∗δ(n)=h(n) となる。このときの出力 h(n) がインパルス応答と呼ばれる。連続時間においても同様。
復習3:FIR フィルタと IIR フィルタ
伝達関数の形によってフィルタ(システム)は 2 種類に分類される。式 (3) を z 変換すると
Y(z)=H(z)X(z),H(z)=X(z)Y(z) となる。連続時間信号の場合はラプラス変換 (s変換) であり、上式の z が s になった式が導かれる。この H(z) がシステムの伝達関数である。この伝達関数の式の形によって分類すると以下のようになる。
IIR (infinite impulse response) フィルタ
過去の時刻の出力が入力側に戻って、現在の時刻の出力を決める形
H(z)=1+k=1∑Iakz−kb0+k=1∑Jbkz−k FIR (finite impulse response) フィルタ
出力は入力側に戻らず、入力のみで現在の時刻の出力が決まる形
H(z)=b0+k=1∑Jbkz−k 1. インパルス不変法 (impulse invariant method)
アナログフィルタからディジタルフィルタを求める
インパルス不変法とは、アナログフィルタとディジタルフィルタで、インパルス信号を入力したときの出力が変わらないよう(不変になるよう)に設計する方法である。不変であることを図を用いて説明する。
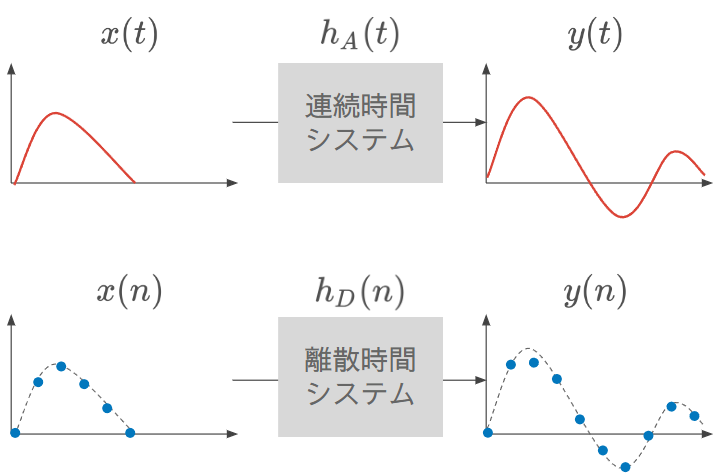
上図において、x(n) はサンプリング周期 T で x(t) を離散化したものとする。すなわち、x(n)=x(nT) である。二つのシステムがありそれぞれの出力を y(t),y(n) としたとき、y(n)=y(nT) であることをここでは不変と呼ぶ。 hD(n)=hA(nT) が不変を満たすことのは自明である。
上記を前提に式を展開する。連続時間システムのインパルス応答 hA(t) の伝達関数を HA(s) とし、この伝達関数が
HA(s)=s−s1a1+s−s2a2+…+s−sNaN で書かれるとする。逆ラプラス変換を用いるとインパルス応答は
hA(t)=a1es1t+a2es2t+…+aNesNt で記述される。離散時間システムのインパルス応答 hD(n) は、このインパルス応答をサンプリング周期 T で離散化すればよいため、
hD(n)=hA(nT)=a1es1nT+a2es2nT+…+aNesNnT である。これを z 変換すると、離散時間システムの伝達関数 HD(z)が求められる。伝達関数を求めるために、インパルス応答の第 i 項に着目すると、
Z[esinT]=n=0∑∞esinTz−n=1−esiTz−11 である。これをすべての項に適用すると、
HD(z)=1−es1Tz−1a1+1−es2Tz−1a2+…+1−esNTz−1aN が得られる。
💡
HA(s)=s−s1a1 のアナログフィルタがある。インパルス不変法を用いてディジタルフィルタに変換し、伝達関数を求めよ。また、その周波数特性の実部と虚部を求めよ。
💡
HA(s)=(s+a)2+b2b のアナログフィルタがある。インパルス不変法を用いてディジタルフィルタに変換し、伝達関数を求めよ。また、その周波数特性の実部と虚部を求めよ。ヒント:式(5)の形に変形できればよさそう。
求めたディジタルフィルタは安定なのか?
フィルタの安定性は極 (pole) で判定できる。いま、アナログフィルタの i 番目の極を
si=αi+jβi とする。ラプラス変換で全ての αi について αi<0 であれば、そのフィルタは安定である。式(6) より、対応するディジタルフィルタの伝達関数の極 ziは、
zi=esiT=e(αi+jβi)T である。z 変換で全ての zi について ∣zi∣<1 であれば、そのフィルタは安定である。∣zi∣ は
∣zi∣=e(αi+jβi)T=eαiT⋅ejβiT=eαiT である。αi<0 のとき ∣zi∣<1 である。すなわち、元のアナログフィルタが安定であれば、インパルス不変法により導出されるディジタルフィルタも同様に安定である。
💡
同様の展開により、s 平面における虚数軸 (
α=0) は、z 平面における単位円 (
∣z∣=1) に写像されることになる。
どんなアナログフィルタでも変換できるのか?
インパルス不変法は、アナログフィルタのインパルス応答の離散化に基づいている。そのため、サンプリング定理を満たさなければならない。元のアナログフィルタの最大周波数が fmax [Hz] であるとき、その 2 倍以上のサンプリング周波数を用いなければならない。逆に、サンプリング周波数があらかじめ決まっている場合は、使用できるアナログフィルタの最大周波数は限定されることになる。
この理由より、インパルス不変法で変換できるフィルタはLPF、BPFに限られる。また、その最大周波数(ここでは、阻止域に至る周波数ととらえてよい)がサンプリング定理を満たしていなければならない。
2. 双一次変換 (Bilinear transform)
復習:ラプラス変換 (s 変換) と z 変換の関係
双一次変換の前にラプラス変換と z 変換の関係を思い出そう。ラプラス変換と z 変換はそれぞれ
X(s)X(z)=∫0∞x(t)s−stdt=n=0∑∞x(nT)z−n この 2 つの式において、離散時間信号は連続時間信号をサンプリング周期 T でサンプリングしたものである。この 2 式が等価となるためには、z=esT でなければならない。(この論理はやや突飛しているため、正確な論理展開は z 変換の回を参照されたい)
この関係式を、さらにテイラー展開による1次近似で表すと、
z=esT=e−sT/2esT/2≃1−sT/21+sT/2 となる。この式を s について解くと
s=T21+z−11−z−1 が得られる。この式(11)(12) を、s と z の双一次変換と呼ぶ。双一次変換を用いてアナログフィルタをディジタルフィルタに変換する場合は、アナログフィルタの伝達関数の周波数 s をこれらの式を用いて z に変換すればよい(詳しい手順は後述)。
双一次変換の意味するところ:周波数の対応
式 (11) に示すように、連続時間信号のすべての周波数は離散時間信号の周波数に対応することになる。では、どのような対応になるだろうか。いま、連続時間信号の角周波数を ωA、離散時間信号の角周波数を ωD とし、双一次変換の式にs=jωA,z=ejωDT を 代入すると、
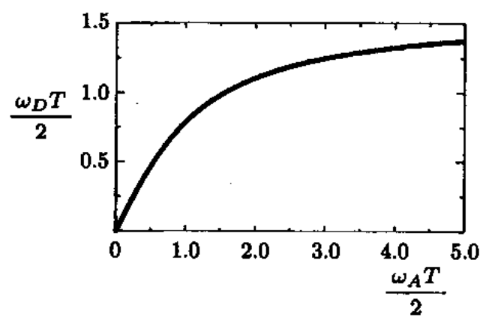
jωAωA=T21+ejωDT1−e−jωDT=T2tan(ωDT/2) となる。この式が意味するのは 2 つである。
- 連続時間信号の角周波数は、離散時間信号の角周波数と非線形に対応する。なお、インパルス不変法では線形に対応に対応する。
- 連続時間信号のすべての周波数は、arctan によって一定範囲に変換され、離散時間信号の周波数となる。時間の都合上省略するが、この効果によってインパルス不変法で触れたないキスと周波数の問題は発生しない。
求めたディジタルフィルタは安定なのか?
結論から言えば、インパルス不変法と同様に、元のアナログフィルタが安定であれば、双一次変換で求めたディジタルフィルタも安定である。
💡
元のアナログフィルタが安定であれば、双一次変換で求めたディジタルフィルタも安定であることを証明せよ。具体的には、式(11) に
s=σ+jω を代入し、
σ<0 であれば
∣z∣<1 であることを導け。
アナログフィルタからディジタルフィルタを求める
具体的な数字を用いて設計してみよう。カットオフ角周波数(遮断角周波数)が ωA のアナログフィルタ
H(s)=s+ωAωA がある。これをもとに、サンプリング周波数 8 kHz、カットオフ周波数(遮断周波数)が 1 kHz のディジタルフィルタを作りたい。この時のアナログフィルタの特性(すなわちカットオフ周波数 ωA )と、ディジタルフィルタの伝達関数を求めよう。
step 1: アナログフィルタの特性を求める
式(14) を用いる。T=1/8000,ωD=2π⋅1000 (カットオフ角周波数) を代入すると、
ωA=2⋅8000⋅tan(2π8000⋅21000)≃6627 故に、アナログフィルタは
H(s)=s+66276627 となる。なお、このカットオフ角周波数からカットオフ周波数を求めると
6627[rad/s]/2π[rad]≃1055[Hz] となり、アナログフィルタのカットオフ周波数とディジタルフィルタのカットオフ周波数が異なることを確認できる。
step 2: 双一次変換を用いてディジタルフィルタの伝達関数を求める
式(15)に式(12)を代入し整理すればよい。
HD(z)=HA(s)∣s=T21+z−11−z−1=22627−9373z−16627(1+z−1)
3. まとめ
- アナログIIRフィルタをディジタルフィルタに変換したい
- インパルス不変法は、アナログフィルタをサンプリングする方法である。単純な方法で変換できるが、サンプリング定理を満たす範囲のフィルタのみを扱える。
- 双一次変換は、アナログフィルタの周波数をディジタルフィルタの周波数に対応させる方法である。サンプリング定理を自動的に満たすが、周波数の対応が非線形であることに注意する。


