ディジタル信号処理第07回-2 窓関数

💡

データを区切って離散フーリエ変換するにはどうしたら？ → 窓関数

0. 復習：フーリエ変換とは時間信号を複素正弦波の和で表す

単一周波数の正弦波をフーリエ変換したら、単一の周波数のみが非零の値になるはずだ。正確には”複素”正弦波を用いるため、正の周波数と負の周波数の2つが現れる。

\sin(\omega t) = \frac{1}{2j}\left(e^{j\omega t} - e^{-j\omega t} \right)

カッコ内の第1項が正の周波数、第2項が負の周波数を表す。それらの係数が周波数表現である。

💡

このような直感を身に着けると、フーリエ変換の理解が進む

1. 離散時間信号を切り出して離散フーリエ変換する

ここで2 つの信号を考える。左は時間信号、右はパワースペクトルである。

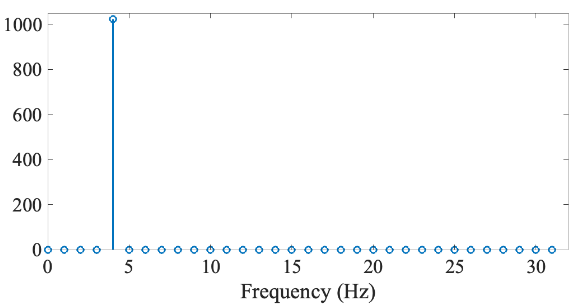
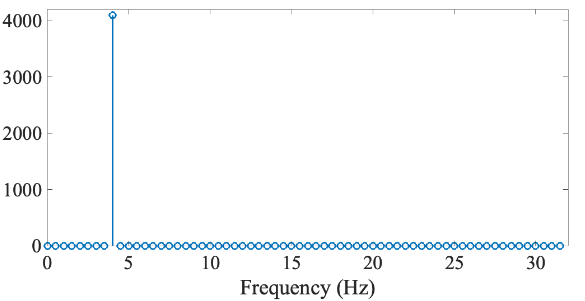
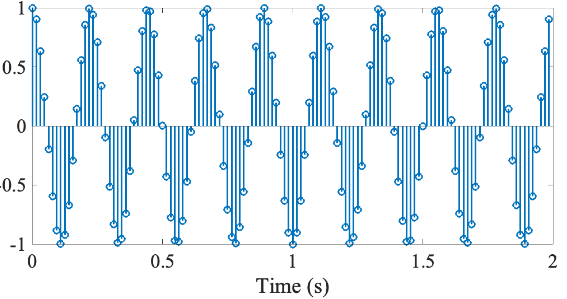
ケース①ー信号①：4 Hz の正弦波、1秒間

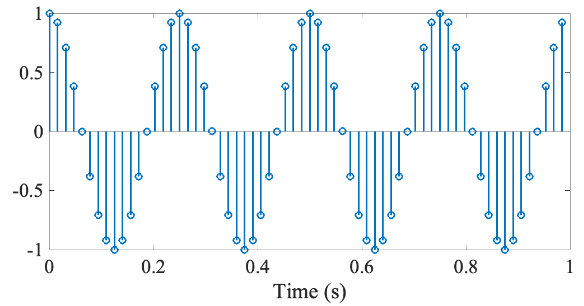
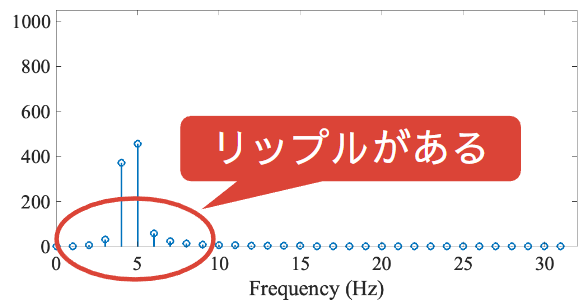
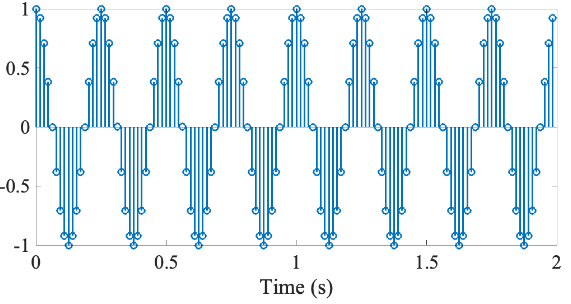
ケース①ー信号②：4.5 Hz の正弦波、1秒間

復習を踏まえれば、これらを離散フーリエ変換すると単一周波数のみが非零になるはずだ。しかしながら、信号②のほうはそうなっておらず、近傍の周波数に染み出しが起きている。この染み出しをリップル（リプル）と呼ぶ。

　では今度は、周波数を変えずに信号の長さを2倍にした結果を見てみよう。

ケース②ー信号①：4 Hz の正弦波、2秒間

ケース②ー信号②：4.5 Hz の正弦波、2秒間

信号の長さを変えただけなのに、こちらは直感に合う。これらの違いは何だろうか？これに答えるために，各信号が切り取り区間の中に何周期分入っているかを調べよう．

ケース①： 1秒

信号①： $1 / (1 / 4) = 4$ [周期]

信号②： $1 / (1 / 4.5) = 4.5$ [周期]

ケース②： 2秒

信号①： $2 / (1 / 4) = 8$ [周期]

信号②： $2 / (1 / 4.5) = 9$ [周期]

これを見る限り，入っている周期がぴったり整数周期にならないときに，前述した問題が生じているようだ．この理由には「離散フーリエ変換が信号の周期性を仮定していること」が関係する。

　前回までで勉強したように離散フーリエ変換は切り出した時間区間の外側で信号が周期的に繰り返されると仮定している。すなわち、区間の端で不連続が起きると所望した結果にならない。ではどうする？

信号の周期ぴったりになるように時間区間を変える？ → 周波数成分を知るために離散フーリエ変換するのに、離散フーリエ変換しないと時間区間を求められない？あまり現実的でない

区間の端が連続的につながるように信号の切り出し方を変えればよいのでは？ → 窓関数

2. 窓関数：信号を切り出すための関数

窓関数 (window function)とは信号に乗算して切り出す関数である。窓関数の多くは両端が 0 に近くなるように設計される。

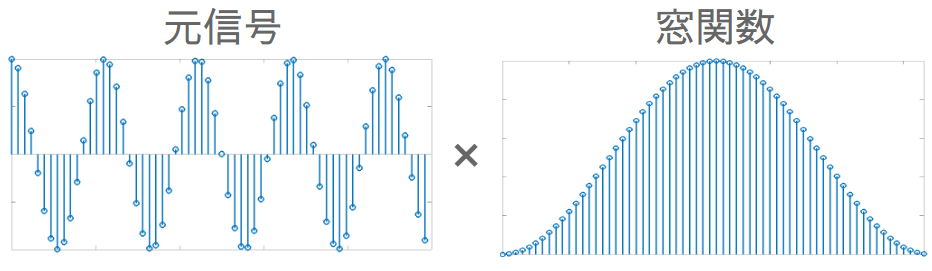
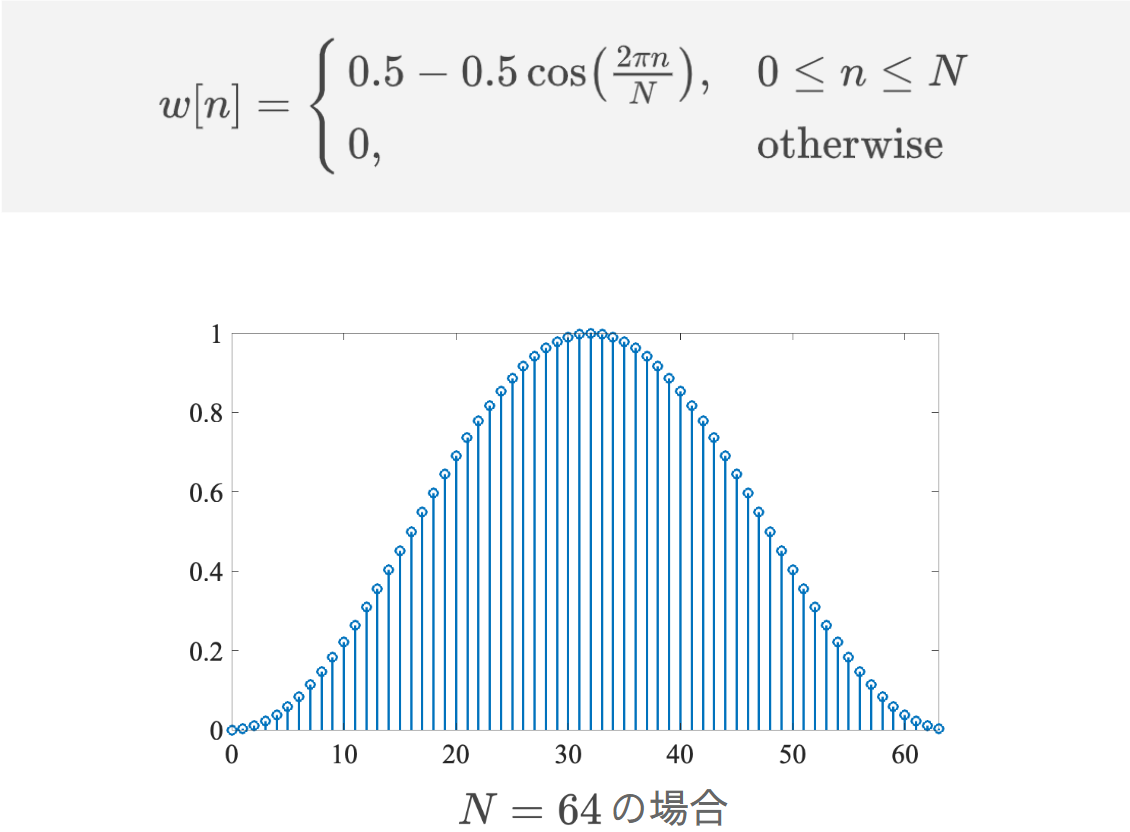
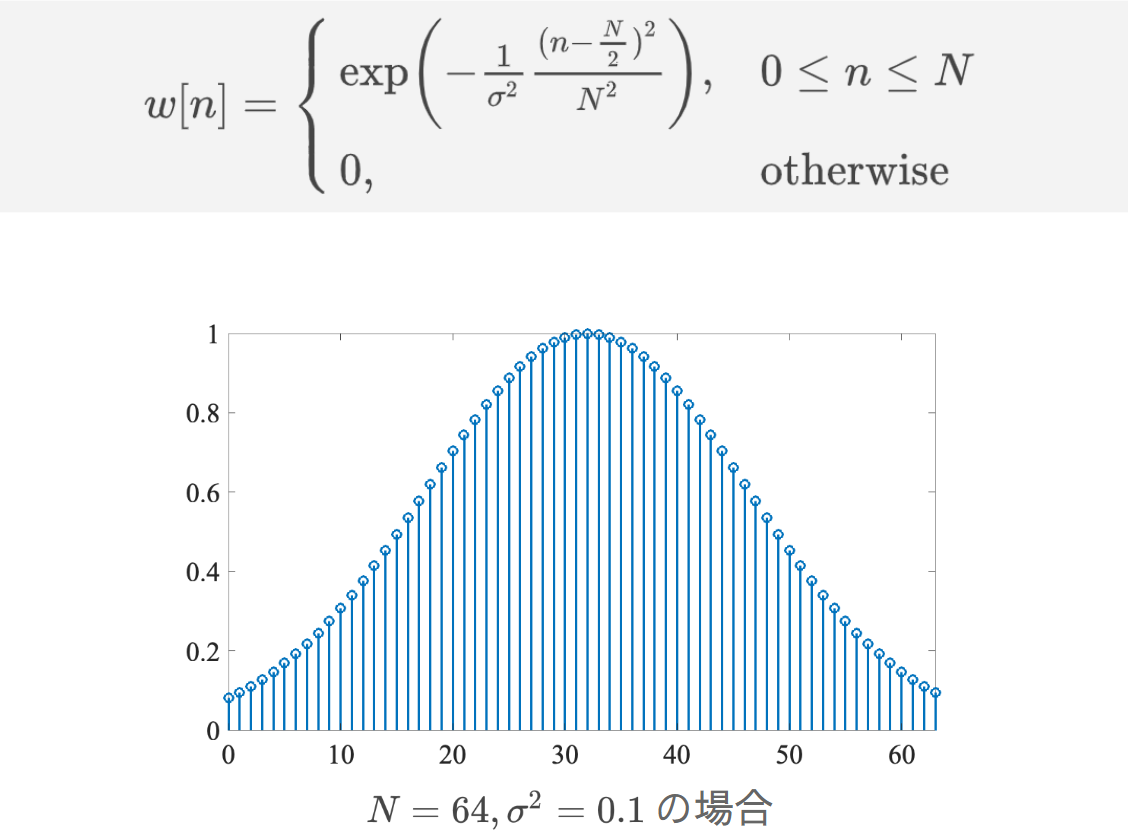
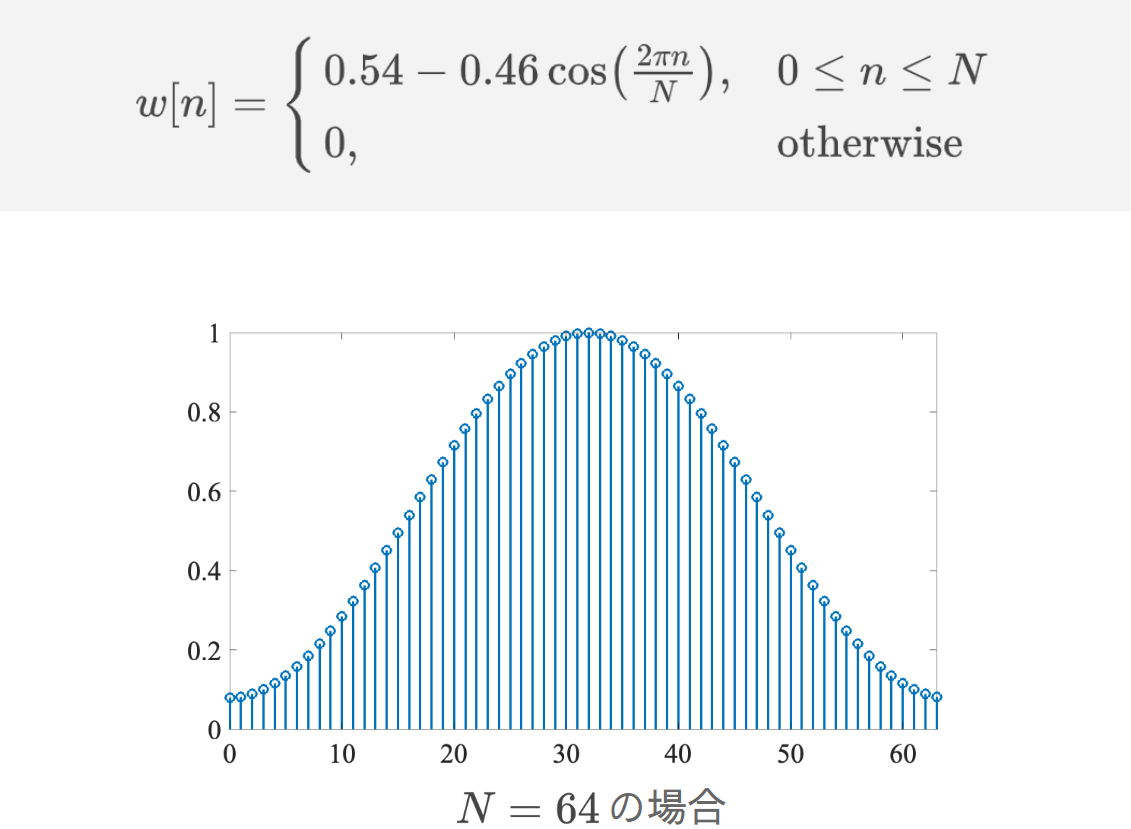
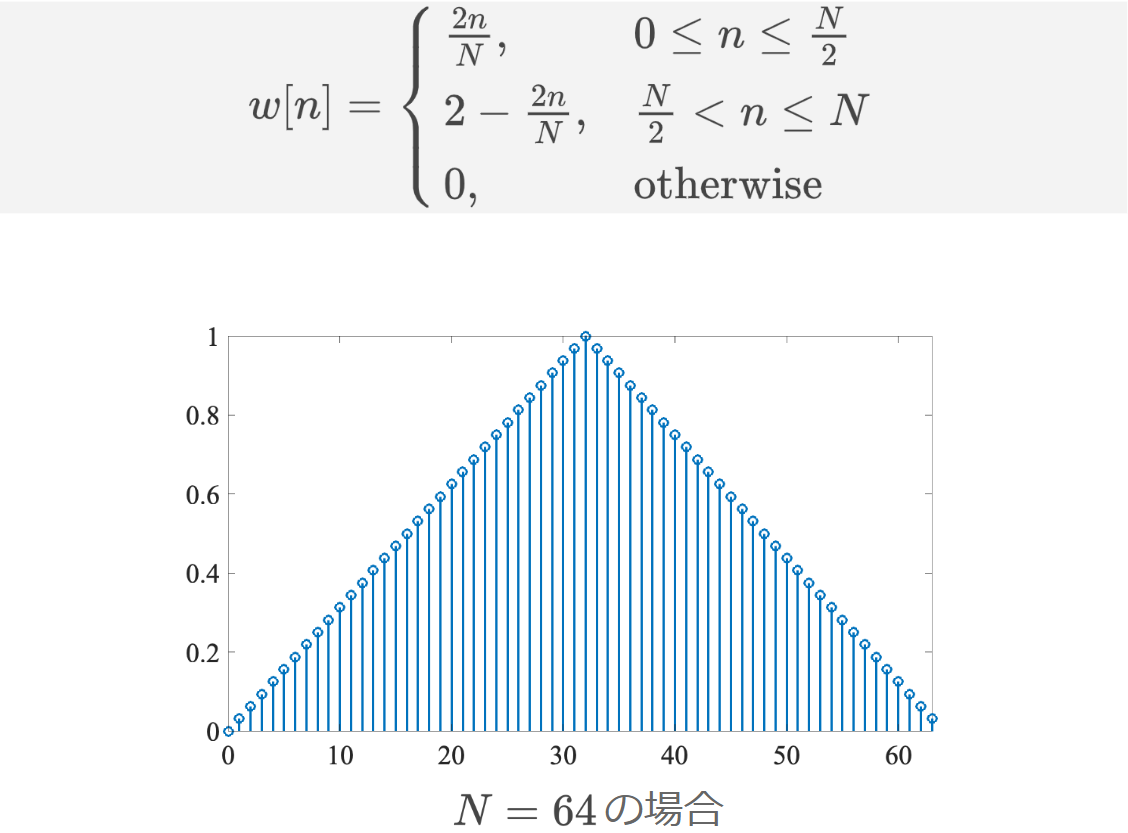
窓関数にはいくつかの種類がある。

ハニング窓

ガウス窓

ハミング窓

三角窓（バートレット窓）

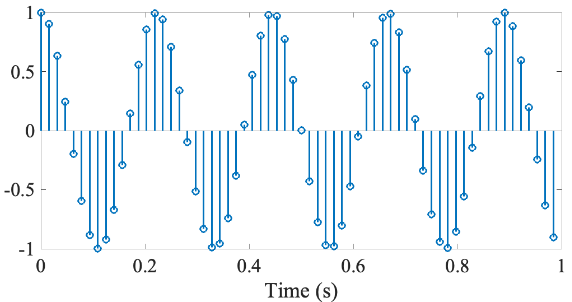
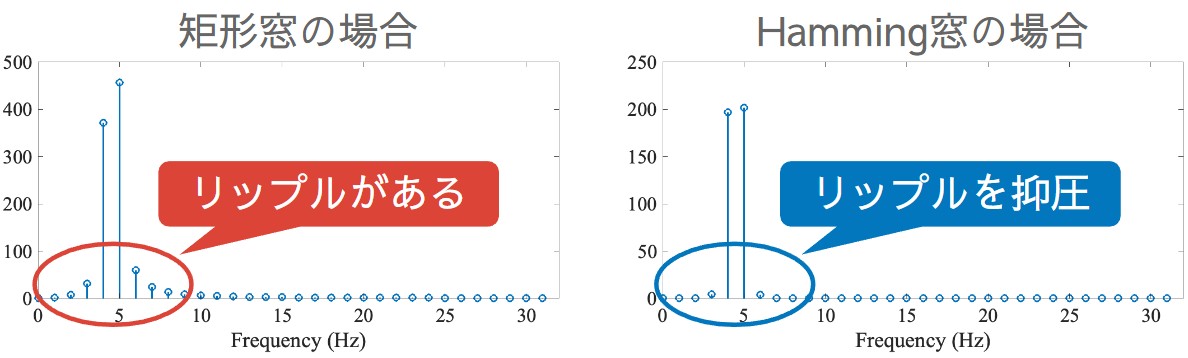
これらのような窓関数をかけると、前述したリプル現象を抑圧できる。なお、前述したような単純に信号を切り出すことは、矩形窓（四角形の窓）という窓関数で切り出することと等価である。下図は、矩形窓で切り出した場合とハミング窓で切り出した場合の比較である。これまで議論されたリプルが軽減されていることがわかる。

💡

窓関数は信号を変えることに相当するため、得られる周波数表現も変わる。種々の窓関数のうち、どれを選べばよいだろうか？本講義では省略するが、興味のある人は、周波数分解能とダイナミックレンジについて調べてほしい。

3. 短時間フーリエ変換

時々刻々と変化する時系列信号を考えよう。例えば人間の音声のように「あいうえお」と発音内容が変わる信号だ。このような信号全体に対して離散フーリエ変換することは、あまり意味がない。なぜか？

　離散フーリエ変換は信号を複素正弦波の和で表すものであり、その振幅・初期位相などは時間で変化しない。故に、時々刻々と変化する信号全体を一気に離散フーリエ変換すると、変化する要素をとらえられない。

　そこで、信号を短時間の時間区間ごとに切り出して、それぞれの区間で離散フーリエ変換すればよいことになる。この切り出しは、前述した窓関数で実現できる。

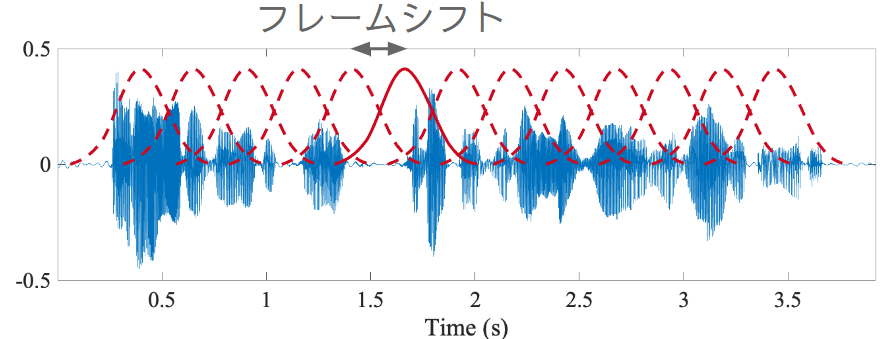
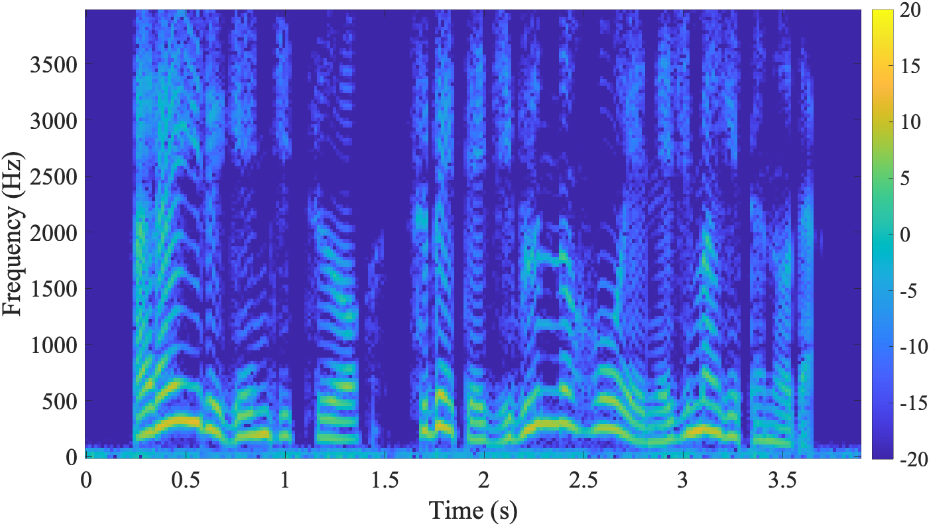
　この変換のことを短時間フーリエ変換 (short-time Fourier transform; STFT) という。この STFT を用いると、各時間-周波数でどのような振幅値を持っているかを示す振幅スペクトログラムを描画することもできる。下図は、横軸が時刻、縦軸が周波数、色の明暗が振幅を表す。