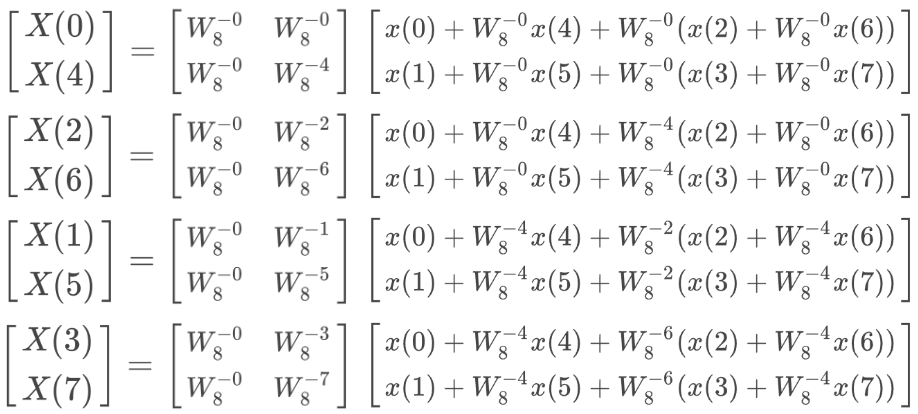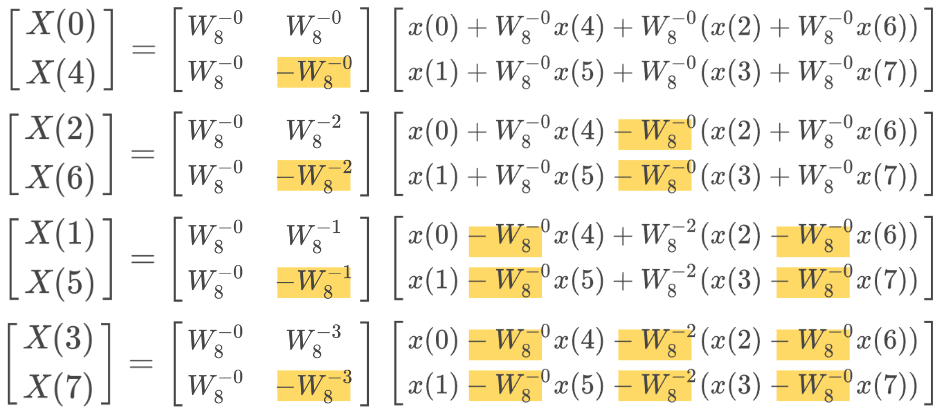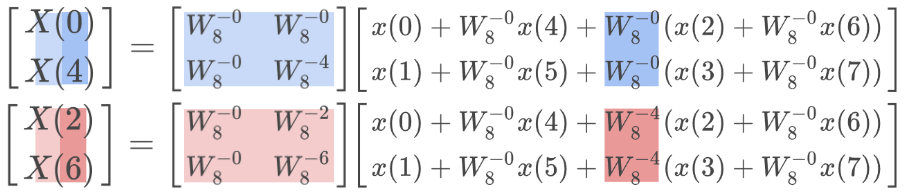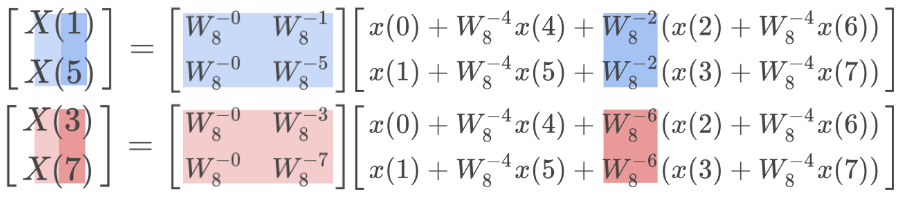ディジタル信号処理 第07回-1 FFT

💡
離散フーリエ変換は計算量が多いからどうにかしたい！ → FFT（高速フーリエ変換）

0. 復習：離散フーリエ変換

離散フーリエ変換の定義

　離散時間信号 (ディジタル信号) を x(n)x(n) とする。nn  は時刻のインデックス（整数）であり、00 から N−1N-1 までの値をとる（信号長は NN）。次式に示す離散フーリエ変換（discrete Fourier transform; DFT）によって、信号の周波数表現 X(k)X(k) が得られる。

X(k)=∑n=0N−1x(n)e−j2πkn/N\begin{align} X(k) = \sum\limits_{n = 0}^{N-1}x(n) e^{-j2\pi kn/N} \end{align}

X(k)X(k) は複素数。kk は周波数のインデックス（整数）であり、00 から N−1N-1 までの値をとる。この逆変換は逆離散フーリエ変換（inverse DFT; IDFT）と呼ばれ、次式で記述される。

x(n)=1N∑k=0N−1X(k)ej2πkn/N\begin{align} x(n) = \frac{1}{N}\sum\limits_{k = 0}^{N-1}X(k) e^{j2\pi kn/N} \end{align}

この正変換・逆変換の式は

を表す。

💡
これらを把握すると「離散フーリエ変換の結果が何を表しているのか直感的に説明できる」「フーリエ変換のプログラムを使うときに結果を疑える」能力を身に着けられる

　数学を面白いと思える人向けにおまけの話。なぜ、正変換と逆変換で式の形が微妙に違うのか？具体的には以下の 2 つについて。

これは信号の展開表現（すなわち、なんらかの信号(基底)の和によって、所望の信号を表現すること）に関連する。この基底が正規直交基底であるとき係数は基底同士の内積で計算され、複素数の基底A, Bの内積は、A と B複素共役の積分で計算される。
　離散フーリエ変換では、フーリエ基底
ej2πkn/Ne^{j2\pi kn/N} を用いて信号を表現する。そのときの内積は、基底の複素共役、すなわち e−j2πkn/Ne^{-j2\pi kn/N} を用いて計算される。これが、正変換において負が現れる理由。逆変換だけ 1/N1/N が現れる理由は、フーリエ基底が直交だが正規直交ではないから。すなわち内積をとると NN が現れる（正規直交基底なら 1 になる）ため、その効果を打ち消すために、逆変換のほうに NN を押し付けて正規化している。

行列表現

離散フーリエ変換は行列で表すことができる。

x=[x(0),x(1),…,x(N−1)]⊤X=[X(0),X(1),…,X(N−1)]⊤\begin{align} \bm{x} &= [x(0), x(1), \ldots, x(N-1)]^\top \\ \bm{X} &= [X(0), X(1), \ldots, X(N-1)]^\top \end{align}

のように、離散時間信号と周波数表現を列ベクトルで表したとする。離散フーリエ変換は、変換行列W\bm{W}を用いた線形変換で表すことができる。

X=Wx\begin{align} \bm{X} = \bm{W}\bm{x} \end{align}

この変換行列W\bm{W}の中身を見てみよう。ここで、複素正弦波を以下のように簡易化して表示する。

WNx≔ej2πx/N\begin{align} W_N^{x} \coloneqq e^{j2\pi x/N} \end{align}

この WNxW_N^{x} は複素平面における単位円上で xx の増加に応じて回転するため、回転子ともいう。この回転子を用いると、変換行列W\bm{W}を以下のようにあらわすことができる。

W=[W8−0⋅0W8−1⋅0W8−2⋅0W8−3⋅0W8−4⋅0W8−5⋅0W8−6⋅0W8−7⋅0W8−0⋅1W8−1⋅1W8−2⋅1W8−3⋅1W8−4⋅1W8−5⋅1W8−6⋅1W8−7⋅1W8−0⋅2W8−1⋅2W8−2⋅2W8−3⋅2W8−4⋅2W8−5⋅2W8−6⋅2W8−7⋅2W8−0⋅3W8−1⋅3W8−2⋅3W8−3⋅3W8−4⋅3W8−5⋅3W8−6⋅3W8−7⋅3W8−0⋅4W8−1⋅4W8−2⋅4W8−3⋅4W8−4⋅4W8−5⋅4W8−6⋅4W8−7⋅4W8−0⋅5W8−1⋅5W8−2⋅5W8−3⋅5W8−4⋅5W8−5⋅5W8−6⋅5W8−7⋅5W8−0⋅6W8−1⋅6W8−2⋅6W8−3⋅6W8−4⋅6W8−5⋅6W8−6⋅6W8−7⋅6W8−0⋅7W8−1⋅7W8−2⋅7W8−3⋅7W8−4⋅7W8−5⋅7W8−6⋅7W8−7⋅7]\begin{align} \bm{W} = \displaystyle \left[\begin{array}{cccccccc}W_8^{-0\cdot0} & W_8^{-1\cdot0} & W_8^{-2\cdot0} & W_8^{-3\cdot0} & W_8^{-4\cdot0} & W_8^{-5\cdot0} & W_8^{-6\cdot0} & W_8^{-7\cdot0} \\ W_8^{-0\cdot1} & W_8^{-1\cdot1} & W_8^{-2\cdot1} & W_8^{-3\cdot1} & W_8^{-4\cdot1} & W_8^{-5\cdot1} & W_8^{-6\cdot1} & W_8^{-7\cdot1} \\ W_8^{-0\cdot2} & W_8^{-1\cdot2} & W_8^{-2\cdot2} & W_8^{-3\cdot2} & W_8^{-4\cdot2} & W_8^{-5\cdot2} & W_8^{-6\cdot2} & W_8^{-7\cdot2} \\ W_8^{-0\cdot3} & W_8^{-1\cdot3} & W_8^{-2\cdot3} & W_8^{-3\cdot3} & W_8^{-4\cdot3} & W_8^{-5\cdot3} & W_8^{-6\cdot3} & W_8^{-7\cdot3} \\ W_8^{-0\cdot4} & W_8^{-1\cdot4} & W_8^{-2\cdot4} & W_8^{-3\cdot4} & W_8^{-4\cdot4} & W_8^{-5\cdot4} & W_8^{-6\cdot4} & W_8^{-7\cdot4} \\ W_8^{-0\cdot5} & W_8^{-1\cdot5} & W_8^{-2\cdot5} & W_8^{-3\cdot5} & W_8^{-4\cdot5} & W_8^{-5\cdot5} & W_8^{-6\cdot5} & W_8^{-7\cdot5} \\ W_8^{-0\cdot6} & W_8^{-1\cdot6} & W_8^{-2\cdot6} & W_8^{-3\cdot6} & W_8^{-4\cdot6} & W_8^{-5\cdot6} & W_8^{-6\cdot6} & W_8^{-7\cdot6} \\ W_8^{-0\cdot7} & W_8^{-1\cdot7} & W_8^{-2\cdot7} & W_8^{-3\cdot7} & W_8^{-4\cdot7} & W_8^{-5\cdot7} & W_8^{-6\cdot7} & W_8^{-7\cdot7} \\\end{array}\right] \end{align}

nn 行 kk 列の要素はWN−knW_{N}^{-kn} である。

1. 離散フーリエ変換は「重い」

爆発する計算量

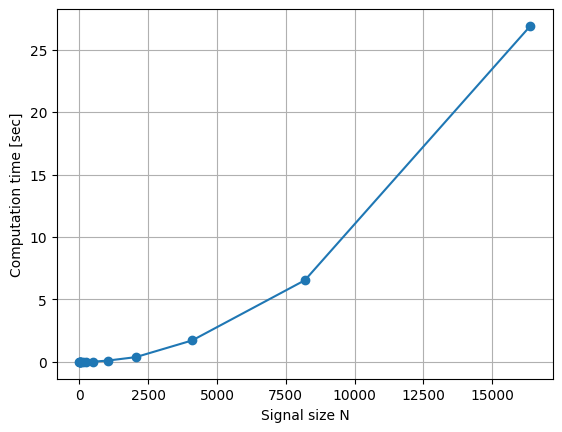
行列W\bm{W}のサイズは N×NN\times N である。すなわち、掛け算を N2N^2 回実行しなければならない。下図は、様々な信号長 NN に対して Python で計算時間を計測した結果である。

2次関数のように計算時間が伸びており N=16384N=16384 で約 26 秒かかる。音楽信号の場合、48 kHz サンプリングを採用することが多いので、 N=16384N=16384 は約 0.333 秒に対応する。すなわち、0.3 秒の音楽をフーリエ変換するのに 26 秒かかることを示している。

💡
本講義の範囲外だが、離散フーリエ変換（に類するもの）は信号の符号化に用いられる。例えば、生の信号データを保存せずに、離散フーリエ変換を用いて圧縮されたデータを保存する。再生時に0.3 秒 の YouTube 音声を復号して聴くために 26 秒かかっては、とてもやっていけない。

上図が示すように、離散フーリエ変換の計算は非常に重い。もちろん、計算機能力の増加でカバーできる部分はあるが、計算時間が 2 次関数になるものは避けたい…。

　これから紹介する高速フーリエ変換 (fast Fourier transform; FFT)は、新たなフーリエ変換ではなく、得られる結果は離散フーリエ変換と同じである。ただし、変換にかかる計算量を非常に小さくしたものである。

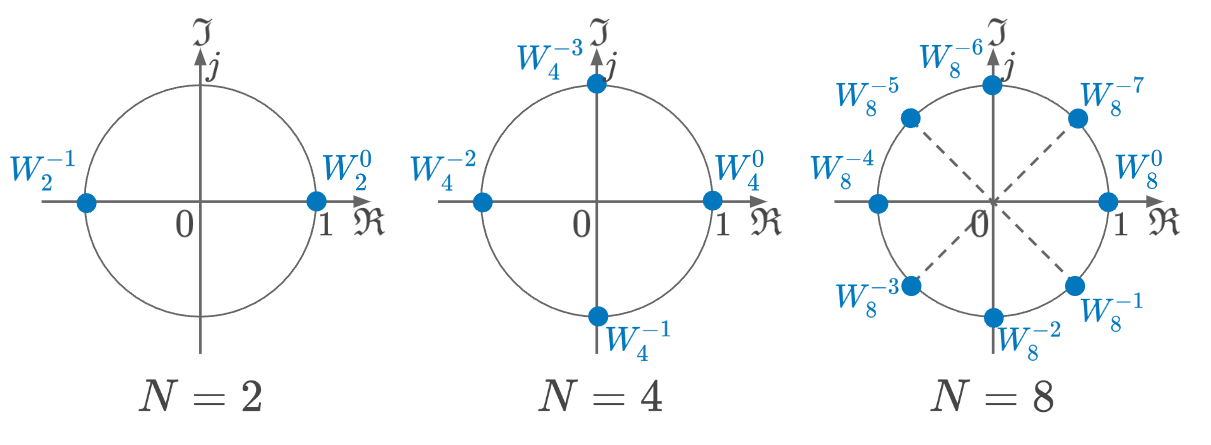
軽くするために回転子の性質を整理しよう

　回転子は、単位円を NN 分割してべき乗数だけ進むものと考えられる。今はべき乗数が負の方向に増えるので、反時計回りに進むと仮定する。この回転子におけるべき乗数の和は、2つの回転子の積に書き換えることもできる（WNx+y=WNx⋅WNyW_{N}^{x+y} = W_{N}^{x}\cdot W_{N}^{y}）。この回転子には次の 2 つの性質がある。

対称性

NN が偶数のとき、

WNx+N/2=−WNx\begin{align} W_N^{x + N/2} &= - W_N^{x} \\ \end{align}

である。すなわち、原点を中心に点対称の位置に移動することは、−1-1 をかけることに等しい。回転子の式に代入すれば証明できる。

周期性

MM を整数とすると、

WNx+MN=WNx\begin{align} W_N^{x + MN} = W_N^{x} \end{align}

である。すなわち、単位円を MM 周しても同じ位置に戻る。

2. 離散フーリエ変換から高速フーリエ変換へ

変換行列を可視化してみよう

　変換行列 W\bm{W} は以下のように可視化できる。ここでは前述した周期性を用いている。

💡
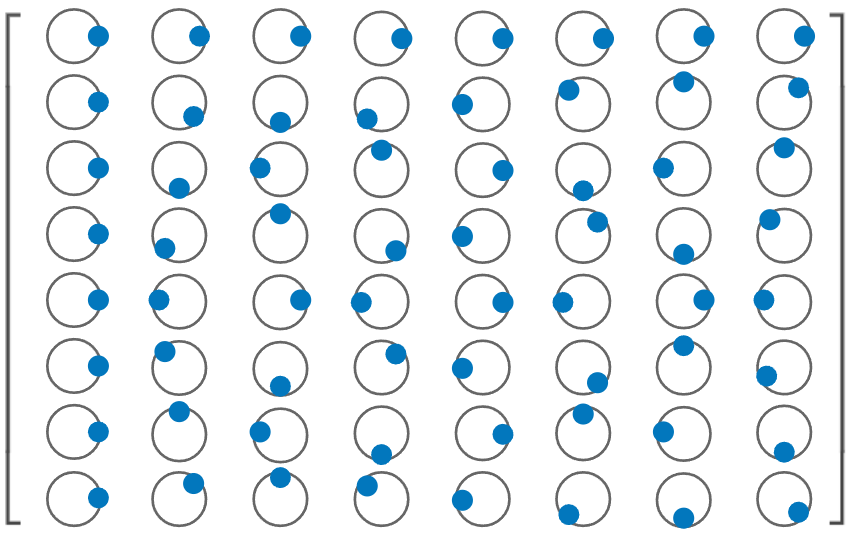
奇数行目と偶数行目それぞれにおいて、左半分と右半分について何かの規則性はないだろうか？

偶数行目：左半分と右半分が同じ（W80W_{8}^{0} ずれている）

奇数行目：左半分と右半分が半周期（W8−4W_{8}^{-4} ）ずれている。

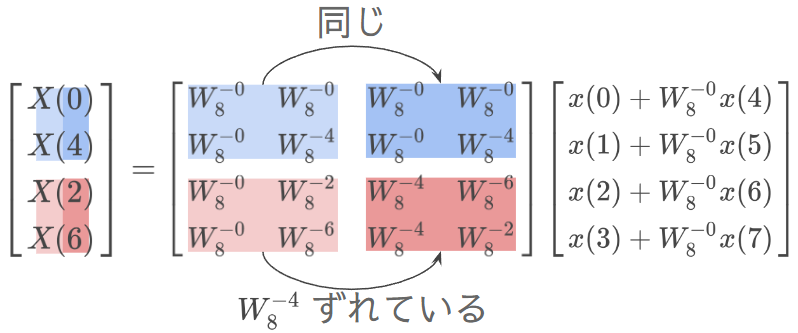
行列を変形してみよう（1段階目）

　いま、薄い青、濃い青、薄い赤、濃い赤の4つの行列要素がある。この 4 つをそれぞれまとめ上げるように、行列を並び替えてみよう。並び替えたことでX\bm{X}の順番が変わったことに注意する。

薄い青と濃い青、薄い赤と濃い赤の関係を思い出すと、この式は以下のように書き換えられる。

W80=1,W8−4=−1W_8^{0} = 1, W_8^{-4} = -1 なので、x[0]+x[4],x[0]−x[4]x[0] + x[4], x[0] - x[4] のように書き換えることもできる。

💡
薄い青と薄い赤の行列要素が、元の変換行列の要素に似た様子で並んでいるのに気づくだろうか？

行列を変形してみよう（2段階目）

1段階目で 8×88\times8 の行列を4×44\times4の2つの行列に分解できた。同様の手順で、この 4×44\times4 の行列を 2×22\times2 の2つの行列に分解しよう。色の対応が 1 段階目と異なることに注意しよう。

上半分

右半分と左半分の関係を考える

並び替える

書き換える

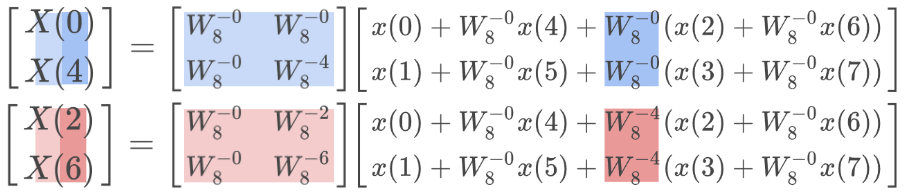
下半分

右半分と左半分の関係を考える

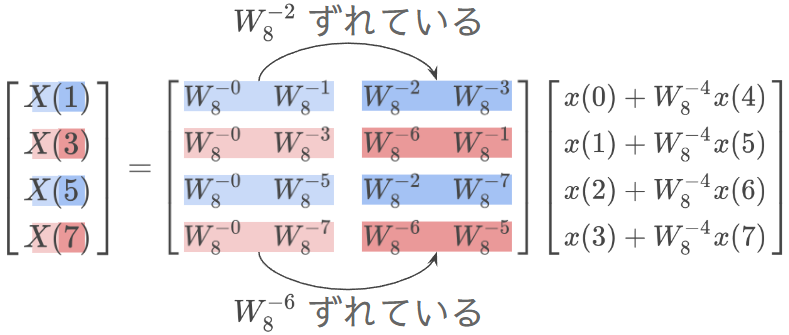
並び替える

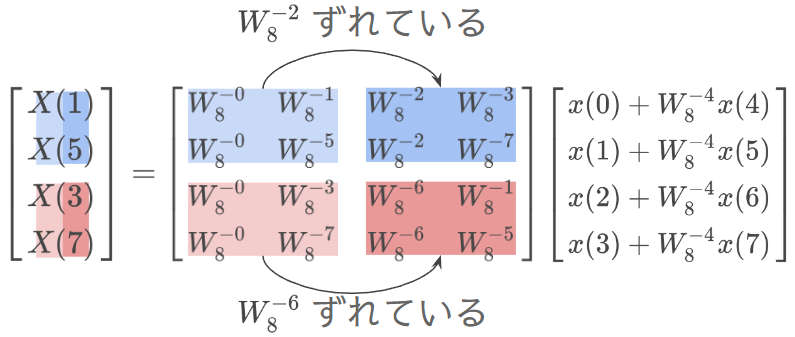
書き換える

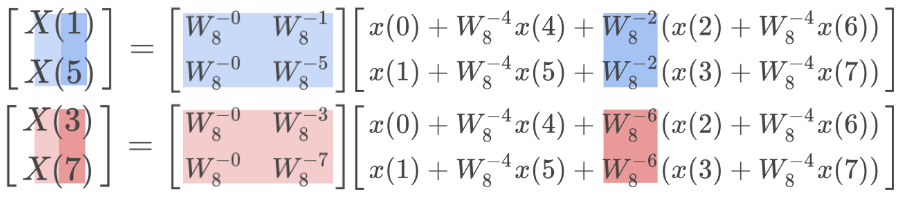
この上半分と下半分の結果を並べると

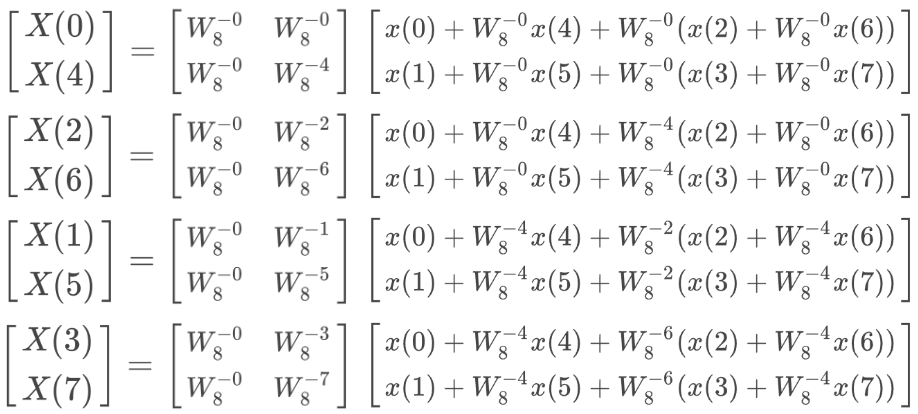
対称性を適用すると

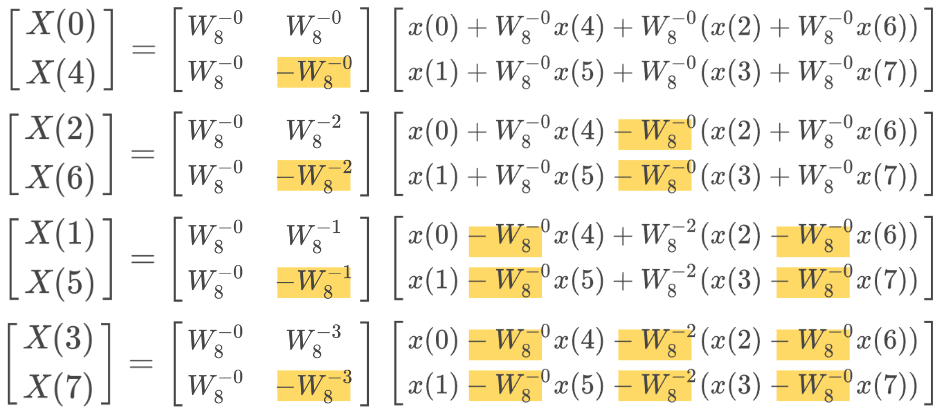
この演算は以下のようなグラフで書くことができる。図の黒丸は、加算ののち乗算を表す。

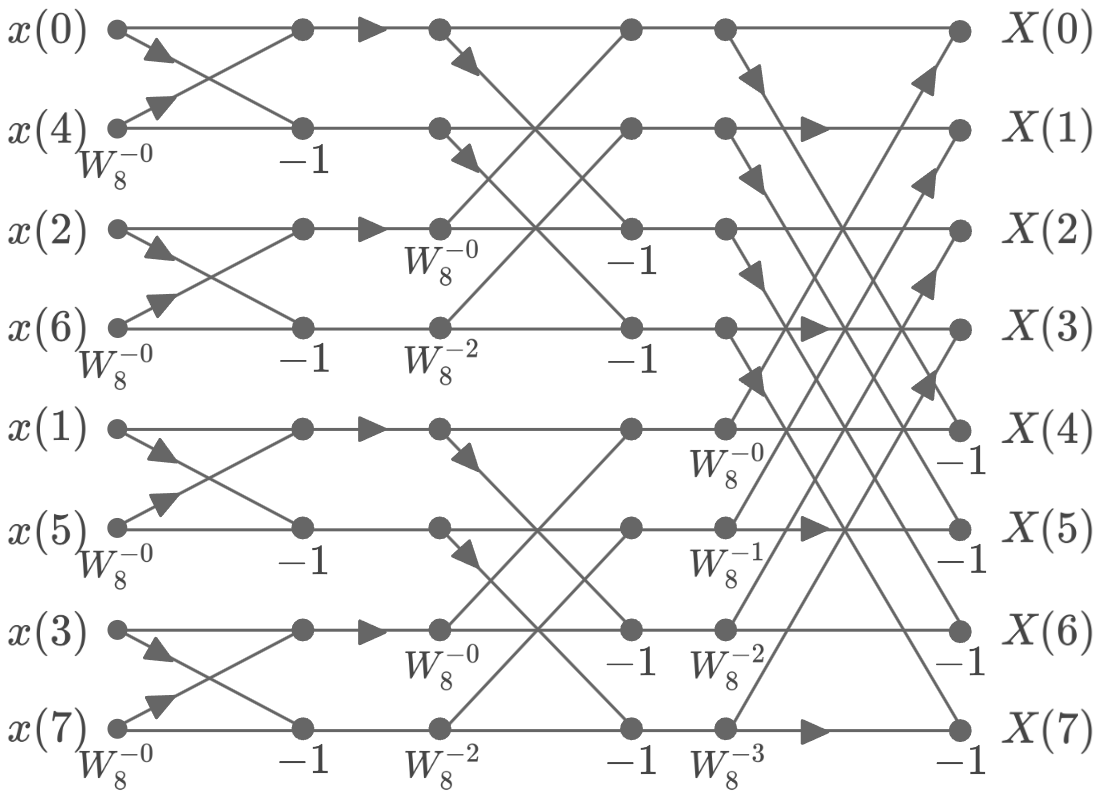
上図に現れる、下図のような演算をバタフライ演算という。高速フーリエ変換は、このバタフライ演算の組み合わせによってなされる。

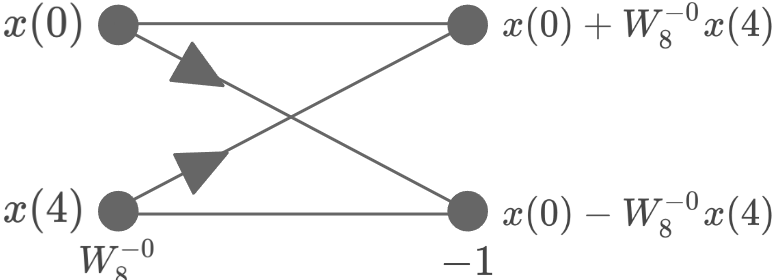
この変更によって、もともと N2N^2 回の計算量（正確にはオーダー）だったものが、Nlog⁡2NN \log_2 N まで減少する。

💡
この計算量の減少は、どれくらい効果があるのだろうか。例えば、N=216=65536N=2^{16} = 65536 (48kHz サンプリングの音楽において約1.37秒)の場合、計算量は何分の一になるだろうか

任意の長さの信号に対して高速フーリエ変換を用いるために　

　高速フーリエ変換は、長さが 2 のべき乗の信号のみに適用できる。しかしながら、一般に信号の長さは 2 のべき乗とは限らない。では、そのような信号に対して高速フーリエ変換を適用するにはどうしたらよいだろうか？

　一つの方法は零詰め (zero padding) である。すなわち 2 のべき乗の長さになるように信号の末尾を 0 で埋める。

💡
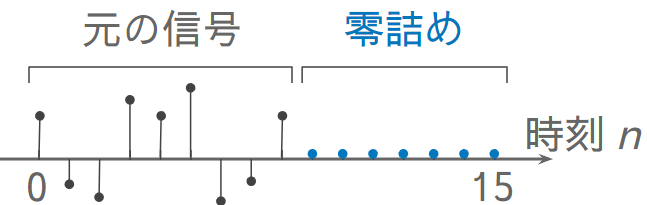
Python における FFT は numpy （下記URL参照）を用いることが多い。この実装のドキュメントでは、信号長に関する言及はあるだろうか。
numpy.fft.fft — NumPy v1.26 Manual
This function computes the one-dimensional n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm [CT].
https://numpy.org/doc/stable/reference/generated/numpy.fft.fft.html

信号の並び替えをビットリバースで実装する

高速フーリエ変換を実行するには、時間信号の順番を並び替える必要がある。計算機上では、これをビットリバースで簡単に実現できる

💡
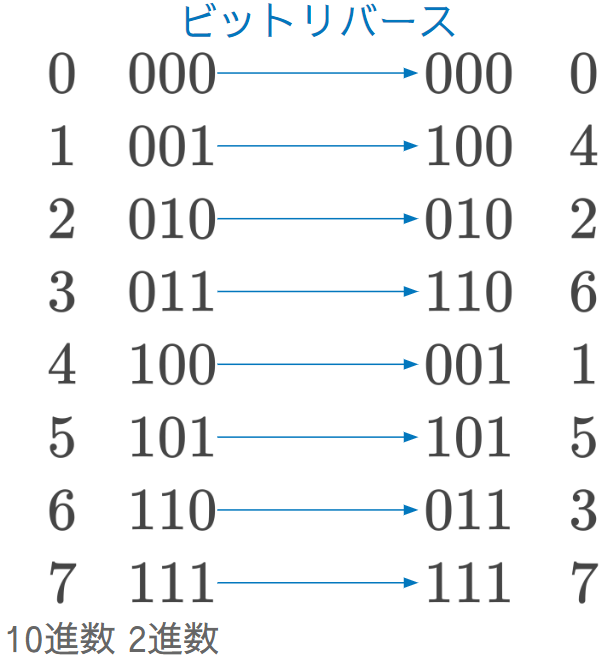
このページで紹介したのは、Cooley-Tukey 型 FFT と呼ばれるものであり、一般的に FFT といえば Cooley-Tukey 型を指す。ほかにどんな型があるだろうか？

3. まとめ